Question 1161537: If P(X) = 0.54, P(Y) = 0.36 and P(X and Y) = 0.27, what is the value of P(X/Y)? Is it the same as P(Y/X)?
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
By the definition of the conditional probability,
P(x | Y) = P(X ∩ Y) / P(Y).
Substitute the given numbers and calculate
P(X | Y) = 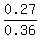 = =  = 0.75.
From the other side,
P(Y | X) = = 0.75.
From the other side,
P(Y | X) = 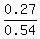 = =  = 0.5.
As you see from my calculations, P(X | Y) is NOT EQUAL to P(Y | X). = 0.5.
As you see from my calculations, P(X | Y) is NOT EQUAL to P(Y | X).
Solved, answered, explained and completed.
----------------
On conditional probability, see the lessons
- Conditional probability problems
- Conditional probability problems REVISITED
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Solved problems on Probability"
and "Additional problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
/\/\/\/\/\/\/\/
For students, who learn the conditional probability for the first time in their life,
it is REALLY difficult to comprehend its meaning.
Imagine a standard Venn diagram as two intersected circles, having some common area.
Call these circles X and Y; then the common area is their intersection (X ∩ Y).
+-------------------------------------------------------------------------------------------------------+
| The conditional probability P(X | Y) is the ratio of the common area to the area of the circle Y. |
| |
| The conditional probability P(Y | X) is the ratio of the common area to the area of the circle X. |
+-------------------------------------------------------------------------------------------------------+
After this explanation, you know EVERYTHING on this conception.
|
|
|