Question 1161375: 1) Suppose you want to have $500,000 for retirement. Your account earns 9% interest compounded monthly. If you deposit $200 at the end of each month, how long will it take you to reach your goal? Round to the nearest year.
years
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The formula for an Ordinary Annuity saving account compounded monthly is
FV = 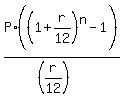 where FV is the future value, P is the annual payment at the end of each year, n is the number of monthly deposits (of months).
So, we need to find " n " from the equation
where FV is the future value, P is the annual payment at the end of each year, n is the number of monthly deposits (of months).
So, we need to find " n " from the equation
 = = 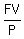 = =  = 2500, which is the same as = 2500, which is the same as
 = 2500.
Rewrite it in this form = 2500.
Rewrite it in this form
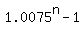 = 0.0075*2500, = 0.0075*2500,
 = 1 + 0.0075*2500 = 19.75.
Take the logarithm base 10 of both sides
n*log(1.0075) = log(19.75)
and calculate
n = = 1 + 0.0075*2500 = 19.75.
Take the logarithm base 10 of both sides
n*log(1.0075) = log(19.75)
and calculate
n = 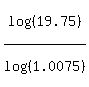 = 399.2 months = 400 months (rounded to the nearest greater integer value) = 33 years and 4 months. ANSWER
CHECK. = 399.2 months = 400 months (rounded to the nearest greater integer value) = 33 years and 4 months. ANSWER
CHECK. 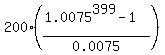 = 499042.54, which is slightly less than 500000; = 499042.54, which is slightly less than 500000;
 = 502985.38, which is slightly greater than 500000. = 502985.38, which is slightly greater than 500000.
Solved, checked, explained and completed.
-----------------------
On ordinary annuity saving plan, see my lessons in this site
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
|
|
|