SOLUTION: Use Newton's Law of Cooling, T=C+(Tsubscript0 - C)e^kt to solve the below: A pizza removed from the oven has a temperature of 450 degrees Fahrenheit. It is left sitting on a room

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Use Newton's Law of Cooling, T=C+(Tsubscript0 - C)e^kt to solve the below: A pizza removed from the oven has a temperature of 450 degrees Fahrenheit. It is left sitting on a room       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1161289: Use Newton's Law of Cooling, T=C+(Tsubscript0 - C)e^kt to solve the below:
A pizza removed from the oven has a temperature of 450 degrees Fahrenheit. It is left sitting on a room that has a temperature of 70 degrees Fahrenheit. After 5 minutes, the temperature of the pizza is 315 degrees Fahrenheit.
a. Use Newton's Law to find the model for the temperature of the pizza T, after t minutes.
answer: 315 = 70 + (5mins - 450)e^kt
b. What is the temperature of the pizza after 25 minutes?
answer - ???
c. When will the temperature of the pizza be 130 degrees Fahrenheit?
answer: ???
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I bake frozen pizzas for my husband very often, so I can figure this out.
T=temperature at time t
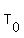T%5B0%5D=temperature at time t=0
C=ambient temperature
The units we use for t and for the temperatures do not matter as long as we are consistent.
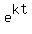At t=0 e%5Ekt=e%5E0=1 makes T=C%2BT%5B0%5D-C=T%5B0%5D
As t approaches infinity ,
e%5Ekt needs to approach 0 ,
so that T approaches C ,
so the constant k must be a negative number.

a. With time in minutes and temperature in degrees Fahrenheit,
the data gives us the equation 315=70%2B%28450-70%29%2Ae%5E%285k%29 ,
or 315=70%2B380%2Ae%5E%285k%29 , if we simplify.
We need to find k , and substitute its value into
T=C%2B%28t%5B0%5D-C%29%2Ae%5Ekt to find the model
(a formula we can use to figure out how long to wait for that pizza to cool).
315=70%2B380%2Ae%5E%285k%29
315-70=380%2Ae%5E%285k%29
245=380%2Ae%5E%285k%29
245%2F380=e%5E%285k%29 I could use 245%2F380=0.6447368421050.644736842105 (or a rounded version of that) in the next equation, but I will let the calculator remember the number and keep crunching numbers.
ln%28245%2F380%29=5k
ln%28245%2F380%29%2F5=k
According to my scientific calculator,
k=-0.08778} (rounded to 4 significant figures).
So, the model is highlight%28T=70%2B380%2Ae%5E%28-0.08778t%29%29
b. After 25 minutes t=25 ,
so we substitute that value into our model to find T for that pizza.
From experience, I say we waited too long.
T=70%2B380%2Ae%5E%28-0.08778%2A25%29
T=70%2B380%2Ae%5E%28-2.1945%29
Using rounded values, e%5E%28-2.1945%29=0.1114 ,so
T=70%2B380%2A0.1114 , and continuing to round, T=70%2B42 ,
so highlight%28T=112%29
After 25 minutes, the temperature of the pizza is 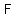112%5EoF%29 .

c. To find out when the temperature of the pizza will be T=130
(in degrees Fahrenheit), we substitute that into our model, getting
130=70%2B380%2Ae%5E%28-0.08778t%29 as the equation to solve.
130-70=380%2Ae%5E%28-0.08778t%29
60=380%2Ae%5E%28-0.08778t%29
60%2F380=e%5E%28-0.08778t%29
ln%2860%2F380%29=-0.08778t
ln%2860%2F380%29%2F%28-0.08778%29=t
and according to my calculator, t=21 .
So, according to our model, to eat the pizza at 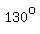130%5EoF , we have to wait highlight%2821minutes%29 .