Question 116124: This is homework and I am having issues.
An ordinary (fair) die is a cube with the numbers 1 through 6 on the sides (represented by painted spots). Imagine that such a die is rolled twice in succession and that the face values of the two rolls are added together. This sum is recorded as the outcome of a single trial of a random experiment.
Compute the probability of each of the following events:
Event A : The sum is greater than 7 .
Event B: The sum is divisible by 2.
Write your answers as exact fractions.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since there are six numbers on each die, there are 6 X 6 = 36 total different results when you roll two dice -- which is the same thing as rolling one die twice in succession.
There is exactly 1 way to get a total of 2: 1 and 1
There are two ways to get 3: 1 and 2, 2 and 1
There are three ways to get 4: 1 and 3, 3 and 1, 2 and 2
four ways to get 5
five ways to get 6
six ways to get 7
five ways to get 8
four ways to get 9
three ways to get 10
two ways to get 11
one way to get 12
For the sum to be greater than 7, it must be 8, 9, 10, 11, or 12 and there are 5 plus 4 plus 3 plus 2 plus 1 ways to get those numbers out of the total of 36.
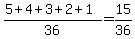
For the total to be even, you have to get a result of 2, 4, 6, 8, 10, or 12, and there are 1 plus 3 plus 5 plus 5 plus 3 plus 1 ways to get these results out of the total of 36 possible.
 . .
|
|
|