What produces holes in rational functions are common zeros between numerator
and denominator with the same multiplicity.
So we try to factor the numerator and denominator by looking for potential zeros
of the numerator and denominator.
We factor the numerator. ±1 are always a potential zeros, so we begin with 1.
1 | 5 8 -11 -14
| 5 13 2
5 13 2 -12
That fails. We try -1
-1 | 5 8 -11 -14
| -5 -3 14
5 3 -14 0
So -1 is a zero of the numerator. The numerator factors as
(t+1)(5t²+3t-14)
Then we factor the numerator further as
(t+1)(t+2)(5t-7)
So we try to see if -1 is also a zero of the denominator
-1 | 20 2 -42 -10 14
| -20 18 24 -14
20 -18 -24 14 0
So we have factored the denominator as
(t+1)(20t³-18t²-24t+14)
We factor further as
(t+1)[2(10t³-9t²-12t+7)]
2(t+1)(10t³-9t²-12t+7)
We investigate to see if -1 is also a zero of 10t³-9t²-12t+7
-1 | 10 -9 -12 7
| -10 19 -7
10 -19 7 0
Yes, -1 is also a factor of 10t³-9t²-12t+7, so it is a factor
of the denominator of the original rational function. So we
have factored the denominator of the original rational function
as:
2(t+1)(t+1)(10t²-19t+7)
We factor further as
2(t+1)(t+1)(2t-1)(5t-7)
Thus the original function with numerator and denominator
completely factored is
So we see that -1 is a common zero of the numerator and
denominator, but they do not have the same multiplicity,
so they produce a vertical asymptote, not a hole.
The only other common zero is 7/5 and both have multiplicity
1. Therefore there is a hole at t=7/5.
The y-coordinate of the hole is the value of the rational
function with all common factors canceled, and the t-coordinate
substituted for t:
We cancel common factors:
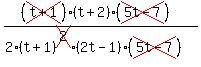
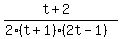We substitute t=7/5
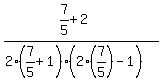
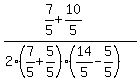
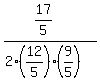
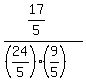
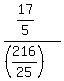
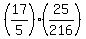Cancel the 5 into the 25
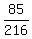So the hole is the point
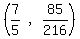Edwin
