Question 1161126: You take the four Aces, four $2$'s, and four $3$'s from a standard deck of 52 cards, forming a set of $12$ cards. You then deal all $12$ cards at random to four players, so that each player gets three cards. What is the probability that each player gets an Ace, a $2$, and a $3$?
The answer is not 27/123200 which is what I got. how I got that was from
The total number of ways to split 12 cards in this way (12 = 3 + 3 + 3 + 3) is
T = C%5B12%5D%5E4.C%5B12-3%5D%5E4.C%5B12-3-3%5D%5E4.C%5B12-3-3-3%5D%5E3 = C%5B12%5D%5E3.C%5B9%5D%5E3.C%5B6%5D%5E3.C%5B3%5D%5E3 = %2812%2A11%2A10%2A9%2A8%2A7%2A6%2A5%2A4%29%2F6%5E3 = 369600.
The number of favorable splittings is F = 3*3*3*3 = 81.
(You may think about the number of 4-symbol words written using a 3-letter alphabet).
So, the probability under the problem's question is
P = favorable%2Ftotal = F%2FT = 81%2F369600 = 0.000219. I simplified fraction. I need fraction form. Thank you!
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It's best to use only standard keyboard characters when posting your questions. Other characters may make your post difficult or impossible to read.
Another tutor answered this question -- possible from you, or possibly from another student -- and got the same answer you got.
You say the answer you and she got is not right.... Do you know what the answer is supposed to be?
For me, at least, it is aggravatingly easy to come up with a method to solve a combinatorics/probability problem that seems valid but is not. If you have the right answer and post it with your problem, it might help some tutor to guide you to that answer.
Answer by ikleyn(52928)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You take the four Aces, four 2's, and four 3's from a standard deck of 52 cards, forming a set of 12 cards.
You then deal all cards at random to four players, so that each player gets three cards.
What is the probability that each player gets an Ace, a 2, and a 3?
~~~~~~~~~~~~~
Thank you for your comment. Under its influence, I reconsidered and redone my previous solution.
This corrected and re-edited solution is placed below.
Under the previous location
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1161100.html
I also updated my post, so now you see the corrected (and identical) version here and there.
The total number of ways to split 12 cards in triples (12 = 3 + 3 + 3 + 3) is
T = 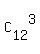 . . . . . .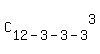 = = 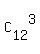 . .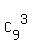 . .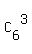 . .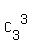 = =  = 369600.
The favorable triples are those that have NO repeating.
More precisely, each favorable splitting is the set of 4 (four) triples, such that no one has repeating.
Now our task is to calculate the total number of such favorable splittings.
In favorable splitting, 1-st triple may contain any one of four Aces, any one of four 2's and any one of four 3's;
so, 1-st triple can be constructed by 4*4*4 = = 369600.
The favorable triples are those that have NO repeating.
More precisely, each favorable splitting is the set of 4 (four) triples, such that no one has repeating.
Now our task is to calculate the total number of such favorable splittings.
In favorable splitting, 1-st triple may contain any one of four Aces, any one of four 2's and any one of four 3's;
so, 1-st triple can be constructed by 4*4*4 =  ways.
2-nd triple may contain any one of the remaining three Aces, any one of the remaining three 2's
and any one of the remaining three 3's; so, 2-nd triple can be constructed by 3*3*3 = ways.
2-nd triple may contain any one of the remaining three Aces, any one of the remaining three 2's
and any one of the remaining three 3's; so, 2-nd triple can be constructed by 3*3*3 =  ways.
next, 3-rd triple may contain any one of remaining two Aces, any one of remaining two 2's
and any one of remaining two 3's; so, 3-rd triple can be constructed by 2*2*2 = ways.
next, 3-rd triple may contain any one of remaining two Aces, any one of remaining two 2's
and any one of remaining two 3's; so, 3-rd triple can be constructed by 2*2*2 =  ways.
finally, 4-th triple may exist only one: there is no any choice for it.
Hence, the number of all different favorable splittings is ways.
finally, 4-th triple may exist only one: there is no any choice for it.
Hence, the number of all different favorable splittings is  .
Therefore, the probability under the problem's question is
P = .
Therefore, the probability under the problem's question is
P =  = =  = = 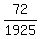 = 0.037403. ANSWER = 0.037403. ANSWER
Solved.
|
|
|