SOLUTION: The count in a bacteria culture was 600 after 15 minutes and 2000 after 30 minutes. Assuming the count grows exponentially, What was the initial size of the culture? Fi

There are different exponential models in use for bacteria growth: a) ekt-models; b) doubling period models with the base of 2, and 
c) general exponential models y = 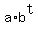,  where t is the time from the starting moment and "b" is some arbitrary base.


In this solution, I will use the general type exponential model y = 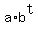 with the base "b".

In this model, "a" is the initial population of bacteria at t= 0.


In our case, we have these two equations from the condition


     = 600     (1)   (after 15 minutes),   and

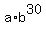     = 2000    (2)   (after 30 minutes)


Divide equation (2) by equation (1). Yopu will get


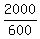     = ,  or

          =  = 3.3333....


From the last equation, 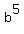  =  = 1.493797  (approximately), and  b =  = 1.083573.


    (  I will keep  and use  b, 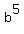   and  , that are the growth factors for 1 minute, and also every 5 minutes and 15 minutes, respectively.

       I will keep and use these values for 5-minute and 15-minutes base periods, since time intervals in this problem are multiple of 5 and 15).


Now I will answer the posed questions, one after another.



Question 1).  During 15 minutes, from 15 minutes to 30 minutes, the population increased from 600 to 2000, 

              so the 15-minutes growing factor is 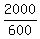  = 3.3333, as we calculated it above.

              Hence, the initial population "a" was  of the population of 600 at t= 15 minutes:

                     a = 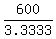 = 180 bacteria.

              So, question 1) is just answered.


Question 2).  The doubling period equation is   = 2,  or  t*log(1.083573) = log(2),  t =  = 8.636 minutes.
              So, question 2) is just answered, too.


Question 3).  The population after 120 minutes is  N(120) =  =  =  = 2,743,265.


Question 4). 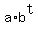  = 14000;  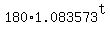 = 14000;  t*log(1.083573) =  = ,

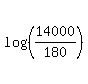              t =  = 54.244 minutes.