Question 1161100: You take the four Aces, four 2's, and four 3's from a standard deck of 52 cards, forming a set of 12 cards. You then deal all cards at random to four players, so that each player gets three cards. What is the probability that each player gets an Ace, a 2, and a 3?
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You take the four Aces, four 2's, and four 3's from a standard deck of 52 cards, forming a set of 12 cards.
You then deal all cards at random to four players, so that each player gets three cards.
What is the probability that each player gets an Ace, a 2, and a 3?
~~~~~~~~~~~~~
The total number of ways to split 12 cards in triples (12 = 3 + 3 + 3 + 3) is
T = 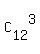 . . . . . .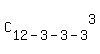 = = 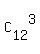 . .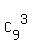 . .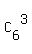 . .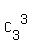 = =  = 369600.
The favorable triples are those that have NO repeating.
More precisely, each favorable splitting is the set of 4 (four) triples, such that no one has repeating.
Now our task is to calculate the total number of such favorable splittings.
In favorable splitting, 1-st triple may contain any one of four Aces, any one of four 2's and any one of four 3's;
so, 1-st triple can be constructed by 4*4*4 = = 369600.
The favorable triples are those that have NO repeating.
More precisely, each favorable splitting is the set of 4 (four) triples, such that no one has repeating.
Now our task is to calculate the total number of such favorable splittings.
In favorable splitting, 1-st triple may contain any one of four Aces, any one of four 2's and any one of four 3's;
so, 1-st triple can be constructed by 4*4*4 =  ways.
2-nd triple may contain any one of the remaining three Aces, any one of the remaining three 2's
and any one of the remaining three 3's; so, 2-nd triple can be constructed by 3*3*3 = ways.
2-nd triple may contain any one of the remaining three Aces, any one of the remaining three 2's
and any one of the remaining three 3's; so, 2-nd triple can be constructed by 3*3*3 =  ways.
next, 3-rd triple may contain any one of remaining two Aces, any one of remaining two 2's
and any one of remaining two 3's; so, 3-rd triple can be constructed by 2*2*2 = ways.
next, 3-rd triple may contain any one of remaining two Aces, any one of remaining two 2's
and any one of remaining two 3's; so, 3-rd triple can be constructed by 2*2*2 =  ways.
finally, 4-th triple may exist only one: there is no any choice for it.
Hence, the number of all different favorable splittings is ways.
finally, 4-th triple may exist only one: there is no any choice for it.
Hence, the number of all different favorable splittings is  .
Therefore, the probability under the problem's question is
P = .
Therefore, the probability under the problem's question is
P =  = =  = = 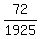 = 0.037403. ANSWER = 0.037403. ANSWER
Solved.
|
|
|