Question 1160991: An antique clock is expected to be worth $350 after 2 years and $530 after 5years.
a) What would be the equation representation for the value of the clock after t years?
b) What will the clock be worth after 7 years?
Found 4 solutions by josgarithmetic, saw, ikleyn, greenestamps:
Answer by josgarithmetic(39621)   (Show Source): (Show Source):
Answer by saw(34)   (Show Source): (Show Source):
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Unfortunately, @josgarithmetic didn't get understanding on what the problem really REQUIRED from the reader.
Therefore, his solution is partly uncompleted, partly irrelevant and partly WRONG.
Taken altogether, these factors make the value of his solution equal to zero (if not negative . . . )
Instead, see my solution below with full explanations.
From the problem's context and by DEFAULT, there is a starting moment (= the reference time) to count the time after it.
So, the problem asks to establish t= 0 at this time moment and find the function of the exponential type for the value
V(t) = 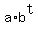 for time "t" counted from this starting reference time moment.
Then from the condition, we have two equations
for time "t" counted from this starting reference time moment.
Then from the condition, we have two equations
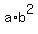 = 350 (1) = 350 (1)
 = 530 (2)
to find the unknown parameters "a" and "b".
Dividing equation (2) by equation (1) (both sides), we get = 530 (2)
to find the unknown parameters "a" and "b".
Dividing equation (2) by equation (1) (both sides), we get
 = =  = 1.514286,
b = = 1.514286,
b =  = 1.148337.
So, we just found parameter "b", and our next step is to find parameter "a".
For it, from the equation (1) you have
a = = 1.148337.
So, we just found parameter "b", and our next step is to find parameter "a".
For it, from the equation (1) you have
a =  = =  = 265.42 (rounded to two decimals).
Now we have EVERYTHING to write the exponential function for the value
V(t) = = 265.42 (rounded to two decimals).
Now we have EVERYTHING to write the exponential function for the value
V(t) =  (3)
with the time "t" counted from the referenced time moment.
Equation (3) is the answer to the first problem's question.
To answer the second and the last problem's question, simply substitute t = 7 into the formula (3) and calculate
V(7) = (3)
with the time "t" counted from the referenced time moment.
Equation (3) is the answer to the first problem's question.
To answer the second and the last problem's question, simply substitute t = 7 into the formula (3) and calculate
V(7) =  = 698.91 (rounded to two decimals).
At this point, the problem is solved completely. = 698.91 (rounded to two decimals).
At this point, the problem is solved completely.
-------------
Dear student @saw,
I know (as you know it) that your knowledge in Algebra are at a rudimentary stage.
Therefore, do not hurry to express your delight by the solution of @josgarithmetic, which is wrong.
Do not hurry to express your delight on the subject without having at least basic knowledge about it,
and keep your emotions with you . . .
Do not pose real experts in FALSE position . . .
/\/\/\/\/\/\/\/
After reading my notices, @josgarithmetic REWROTE his post . . . sweeping tracks . . . and without acknowledgment . . .
It is his usual practice . . .
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I see nothing in the statement of the problem that says the equation for the value of the clock after t years should be exponential, as the other tutors have assumed.
In fact, the statement of the problem is faulty, in that it should specify whether the desired equation is exponential, or linear, or something else.
It is common to use linear depreciation to find the remaining value of a car, or of office equipment; it seems reasonable, then, to use a linear model to find the future value of something that is increasing in value. So on first reading the question (before looking at tutors' responses), it seemed to me the equation should be linear....

The value increases from $350 to $530 -- an increase of $180 -- in 3 years, so the yearly increase is $180/3 = $60.
The value is $350 after 2 years; with an annual increase of $60, that means its starting value is $350-2($60) = $230.
With a starting value of $230 and an annual increase of $60, the equation for the value after t years is

Then the value of the clock after 7 years will be
7($60)+$230 = $420+$230 = $650
|
|
|