SOLUTION: Given p(B)=0.5 and p(AuB')=0.8. What is the value of p(A/B)?

Note that the complement to  (A U B')  is  (A' ∩ B).

Therefore, P(A' ∩ B) = 1 - P(A U B') = 1 - 0.8 = 0.2.



Next,        (A' ∩ B) U  (A ∩ B) = B,  and the sets  (A' ∩ B) and  (A ∩ B)  are disjoint.

Therefore,  P(A' ∩ B) + P(A ∩ B) = P(B),   or

              0.2     + P(A ∩ B) = 0.5,


which implies  P(A ∩ B) = 0.5 - 0.2 = 0.3.



Hence, by the definition of the conditional probability, 

           P(A | B) = P(A ∩ B) / P(B) = 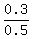 = 0.6.    ANSWER