SOLUTION: Check that (2+i) is a root of z^4+2(z^3)-9(z^2)-10z+50=0. Find the remaining three roots.

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Check that (2+i) is a root of z^4+2(z^3)-9(z^2)-10z+50=0. Find the remaining three roots.      Log On


   

Question 1160754: Check that (2+i) is a root of z^4+2(z^3)-9(z^2)-10z+50=0. Find the remaining three roots.
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

z%5E4%2B2z%5E3-9z%5E2-10z%2B50=0 factor
z%5E4%2B+6z%5E3+%2B10z%5E2+-4z%5E3-24z%5E2-40z+%2B5z%5E2%2B30z+%2B50=0 group
%28z%5E4-4z%5E3%2B5z%5E2%29%2B+%286z%5E3-24z%5E2%2B30z%29%2B%2810z%5E2-40z+%2B50%29=0
z%5E2%28z%5E2-4z%2B5%29%2B+6z%28z%5E2-4z%2B5%29%2B10%28z%5E2-4z+%2B5%29=0
%28z%5E2+-+4+z+%2B+5%29+%28z%5E2+%2B+6+z+%2B+10%29+=+0
use quadratic function to find roots
for %28z%5E2+-+4+z+%2B+5%29=0
z=%28-%28-4%29%2B-sqrt%28%28-4%29%5E2-4%2A1%2A5%29%29%2F%282%2A1%29
z=%284%2B-sqrt%2816-20%29%29%2F2
z=%284%2B-sqrt%28-4%29%29%2F2
z=%284%2B-2i%29%2F2
z=%282%2B-i%29
roots are:
z=2%2Bi ->is a root of z%5E4%2B2z%5E3-9z%5E2-10z%2B50=0
since complex roots always come in pairs, you also have z=2-i

and remaining roots are:

for+%28z%5E2+%2B+6+z+%2B+10%29+=+0
z=%28-6%2B-sqrt%286%5E2-4%2A1%2A10%29%29%2F%282%2A1%29
z=%28-6%2B-sqrt%2836-40%29%29%2F2
z=%28-6%2B-sqrt%28-4%29%29%2F2
z=%28-6%2B-2i%29%2F2
z=%28-3%2B-i%29
roots are:
z=-3%2Bi
z=-3-i


Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
Check that (2+i) is a root of z^4+2(z^3)-9(z^2)-10z+50=0. Find the remaining three roots.
matrix%281%2C3%2C+z%5E4+%2B+2z%5E3+-+9z%5E2+-+10z+%2B+50%2C+%22=%22%2C+0%29

As 1 root is 2 + i, its conjugate/other root is: 2 - i

With  2 + i and 2 - i being roots, we get: z = 2 + i and z = 2 - i, and so, FACTORS are: z - 2 - i and z - 2 + i.

The above expands to 

Using synthetic division or long division of polynomials, we find that the quotient is: 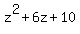z%5E2+%2B+6z+%2B+10.

Now, since this quotient CANNOT be factored, you can use the quadratic equation formula, or "complete the square" to find the other 2 roots.