Question 1160640: Hi
A landscaper wishes to plant a uniform border of tulips on the inside of a rectangular garden with dimensions 12m by 18m.the whole garden will look the best if the area of the tulip border is half the area of the garden.
How wide should the inside border of the tulips be to one decimal place.
Thanks
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the dimensions of the garden are 18 by 12.
to mke a uniform boarder that takes up half the area of the garden, your dimensions of the area within the border would have to be (18 - 2x) by (12 - 2x).
the length and width of the border would be equal to x.
since the area of the garden without the border is 18 * 12 = 216 square meters, then the area of the garden with the border would be half that at 108 square meters.
therefore (18 - 2x) * (12 - 2x) = 108.
simplify this to get:
216 - 36x - 24x + 4x^2 = 108.
combine like terms to get:
216 - 60x + 4x^2 = 108
subtract 108 from both sides of this equation to get:
108 - 60x + 4x^2 = 0
order the terms in descending over of degree to get:
4x^2 - 60x + 108 = 0
divide both sides of this equation by 4 to get:
x^2 - 15x + 27 = 0
factor this quadratic equation to get:
x = 12.908326913196 or x = 2.091673086804
x can't be 12.9..... because then 18 - 2x = 18 - 25.8.... is negative and the dimensions must be positive.
therefore, x has to be equal to 2.091673086804.
that will be the width of the border all around.
that is your solution.
the area of the garden would be equal to (18 - 2 * 2.091673086804) * (12 - 2 * 2.091673086804) = 108 square meters.
the area of the border would have to be 216 minus that = 108 square meters.
here's a picture of what the garden would look like with the border.
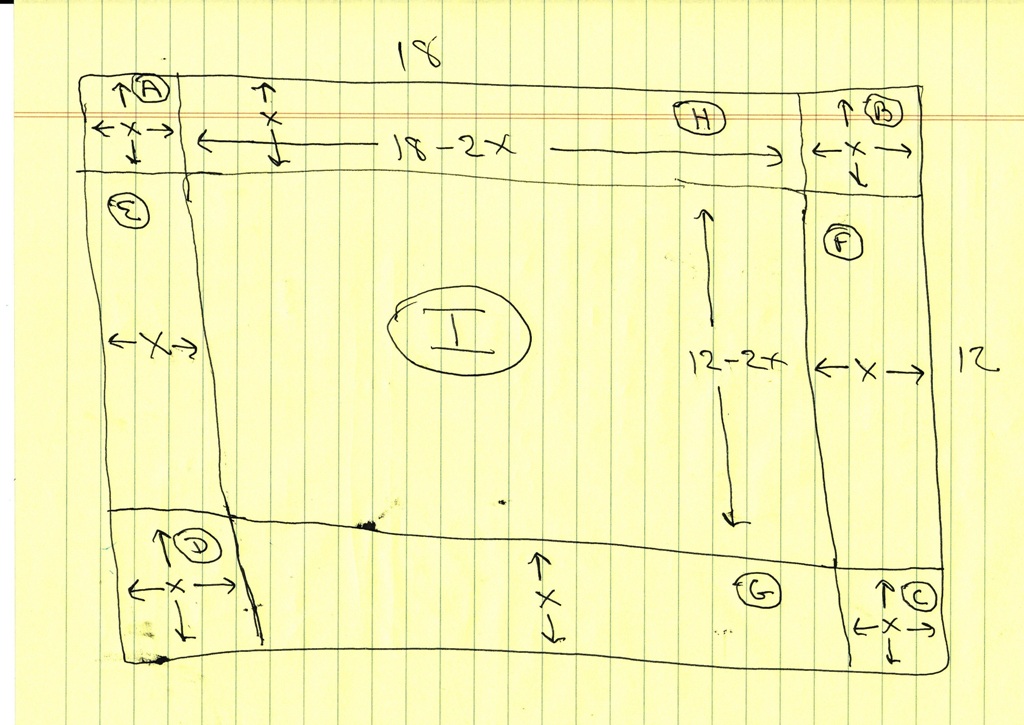
the area of the garden within the border is section I.
the area of that is 108 square meters as calculated above.
the area of the border is the sum of the sections A,B,C,D,E,F,G,H.
the area of sections A,B,C,D, are x^2 = 4.375096302 square meters each.
the area of sections G,H are (18-2x)*x = 28.899922958 square meters each.
the area of sections E,F are (12 - 2x)*x = 16.349884438 square meters each.
the total area of the border is 4 * A + 2 * G + 2 * E = 108 square meters.
it was much easier to get the area of the border by subtracting the area of the garden within the border from the area of the garden without the border.
that made the area of the border equal to 216 - 108 = 108.
|
|
|