SOLUTION: "It took Emily 25 min to ride her bicycle to the repair shop and 1h 15 min to walk back home. If Emily can ride her bicycle 8 km/h faster than she can walk, how far is the repair s

Let "w" be her rate walking, in km/h.

Then the biking rate is (w+8) km/h.


From the condition you have this equation


     = 


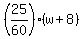saying that the distance is the same in both directions.


From the equation (canceling 60 in the denominators)


    25*(w+8) = 75w

    w + 8 = 3w

    8 = 3w - w = 2w

    w = 8/2 = 4 km/h.


So, the walking rate is 4 km/h;  then the (walking) distance is 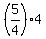  = 5 kilometres.    ANSWER

Let "d" be the distance under the question.


Then from condition you have this equation, connecting rates


     -  =   kilometres per minute.


Simplify by canceling factor 5 in denominators

     -  =  = .


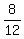Multiply both sides by 15


    3d - d = 10

    2d     = 10

     d     = 10/2 = 5 kilometres,


and you get the same answer for the distance.