|
Question 1160583: Is C correct? I'm checking my answers.
On a residential single lane road there was a wreck that backed up traffic for 4 miles. 70% of the traffic consists of cars and 30% of the traffic consists of trucks. the average distance between vehicles is 3 feet. the average length of a car is 13.5 feet and the average length of a truck is 20 feet. estimate how many vehicles are stuck in the traffic jam.
(hint: there are 5280 feet in 1 mile)
A) 276
B) 896
C) 1172
D) 1412
The image and the question itself are provided in the link here: https://i.imgur.com/0XwjHcy.png
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! i get the following.
traffic jam is 4 miles.
that would be 4 * 5280 = 21120 feet.
the average length of a car is 13.5 feet and the average length of a truck is 20 feet.
allow 3 feet in front of each and the average length of a car is 16.5 feet and the average length of a truck is 23 feet.
70% of the traffic is cars and 30% of the traffic is trucks.
i take this to mean that 70% of the traffic is composed of cars and 30% of the traffic is composed of trucks.
this should mean that the average length of a vehicle will be 70% * 16.5 feet plus 30% * 23 feet = 18.45 feet.
divide 21120 total feet by 18.45 feet average length of a vehicle and you get approximately 1144.715447 vehicles.
this is not one of the selections but it's close enough o 1172 to make that the most likely answer.
i also looked at it another way which i don't think is right, but it does give you one of the selections.
total feet is 4 * 5280 = 21120
if you assume 70% of the traffic is cars, and you multiply 21120 by .7, you get 14784 feet of cars and 6336 feet of trucks.
14784 / 16.5 average length of a car = 896 cars.
6336 / 23 average length of a truck = 276 trucks founded to the next highest integer.
total vehicles is therefore 1172.
i believe traffic means vehicles and not length of vehicles, so i think my first analysis is more accurate, but this is a matter of interpretation.
either way, the selection of 1172 appears to be most accurate, so i think you're ok with selection C.
Answer by ikleyn(52790)  (Show Source):
You can put this solution on YOUR website! .
The formulation of the problem is not self-consistent.
If it requests for ESTIMATION, it should ask which of the four values/options is closest.
Let the number of cars be N, an unknown value.
Then there are (N-1) gaps between the cars, and the basic equation is
0.7*N*13.5 + 0.3*N*20 + 3*(N-1) = 4*5280
which gives
N = 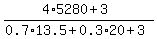 = 1144.9 = 1145 (rounded to the closest integer)
Of the given options, the closest is 1172, option C).
Solved.
|
|
|
| |
