SOLUTION: Floor plans for a building have the four corners of a room located at the points (2,3),(11,6), (-3,18), and (8,21). Determine whether the side through the points (2,3), and (11,6)

Algebra ->  Linear-equations -> SOLUTION: Floor plans for a building have the four corners of a room located at the points (2,3),(11,6), (-3,18), and (8,21). Determine whether the side through the points (2,3), and (11,6)       Log On


   

Question 116051: Floor plans for a building have the four corners of a room located at the points (2,3),(11,6), (-3,18), and (8,21). Determine whether the side through the points (2,3), and (11,6) is parallel to the side through the points (-3,18) and (8,21).
Determine whether the side through the points (2,3) and (11,6) is perpendicular to the side through the points (2,3) and (-3,18).
Help,please.
Thank you, barb neely
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Hello again, Barb,

The principles that are being illustrated in this problem are:

1) Creating equations of lines using the 2-point form of the line.

2) Converting these equations to the point-slope form of the line.

3) Comparing the slopes of lines to determine parallelism and perpendicularity.

First, you need equations of the three lines that we'll call lines A, B, and C.

Using the two-point form of the line: %28y-y%5B1%5D%29=%28%28y%5B1%5D-y%5B2%5D%29%2F%28x%5B1%5D-x%5B2%5D%29%29%28x-x%5B1%5D%29
Line A through points (2,3) and (11, 6).

%28y-3%29=%28%283-6%29%2F%282-11%29%29%28x-2%29, and do the arithmetic to get the point-slope form:
%28y-3%29=%28-3%2F-9%29%28x-2%29
%28y-3%29=%281%2F3%29%28x-2%29 => m%5BA%5D=1%2F3

Now, Line B from (-3,18) to (8,21)
%28y-18%29=%28%2818-21%29%2F%28-3-8%29%29%28x-%28-3%29%29
%28y-18%29=%28%28-3%29%2F%28-11%29%29%28x%2B3%29 => m%5BB%5D=3%2F11

Finally, Line C from (2,3) to (-3,18)
%28y-3%29=%28%283-18%29%2F%282-%28-3%29%29%29%28x-2%29
%28y-3%29=%28%28-15%29%2F%285%29%29%28x-2%29
%28y-3%29=%28%28-3%29%2F1%29%28x-2%29 => m%5BC%5D=-3

Now, your two questions are:

Is line A parallel to line B? Lines are parallel if and only if their slopes are equal. So is 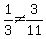m%5BA%5D=m%5BB%5D? 1%2F3%3C%3E3%2F11, therefore the lines are NOT parallel.

Is line A perpendicular to line C? Lines are perpendicular if and only if their slopes are negative reciprocals of each other. So does m%5BA%5D=%28-1%29%2Fm%5BB%5D? 1%2F3=%28-1%29%2F%28-3%29, therefore the lines ARE perpendicular.

Drawing a diagram may show you that this result makes sense:
Line A is the red one, Line B is the green one, Line C is the blue one. You can see that A and B are almost, but not quite parallel, and A and C look perpendicular which are the results that we got algebraically.



Hope that helps,
John