SOLUTION: the sum of the square of 2 consecutive odd positive integers is 209. find the integers.

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: the sum of the square of 2 consecutive odd positive integers is 209. find the integers.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 116046: the sum of the square of 2 consecutive odd positive integers is 209. find the integers.
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
If one of the integers is n, then the other one is n + 2, and their squares are 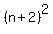n%5E2 and %28n%2B2%29%5E2.

Then the sum of the squares is:
n%5E2%2B%28n%2B2%29%5E2=209

Expand the binomial and simplify:
n%5E2%2Bn%5E2%2B4n%2B4=209
2n%5E2%2B4n%2B4=209
2n%5E2%2B4n-205=0, and now you have a problem because this equation does not have rational roots, which means there is no solution to the problem as you stated it.

However, not being satisfied with that result, I did a little 'easter-egging' and discovered that 11%5E2%2B13%5E2=290 and concluded that you made a small typographical error when you typed the problem.

So, let's start over:

If one of the integers is n, then the other one is n + 2, and their squares are 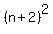n%5E2 and %28n%2B2%29%5E2.

Then the sum of the squares is:
n%5E2%2B%28n%2B2%29%5E2=290

Expand the binomial and simplify:
n%5E2%2Bn%5E2%2B4n%2B4=290
2n%5E2%2B4n%2B4=290
2n%5E2%2B4n-286=0
n%5E2%2B2n-143=0
%28n%2B13%29%28n-11%29=0

So n = 11 or n = -13. But we can eliminate the -13 result because we are looking for consecutive odd POSITIVE integers. Therefore, the first integer is 11 and the second is 11 + 2, or 13.

Please be careful and review your input for accuracy in the future.

Hope that helps,
John