.
I will show you two ways to solve this problem.
Proof 1.
There is an identity, which is valid for any real or complex number w
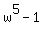 =
=  (1)
You may prove it directly, by making FOIL.
OR you may know it from the formula for the sum of a geometric progression.
In any way, I assume you know it.
Next step. If w is the root of the equation
(1)
You may prove it directly, by making FOIL.
OR you may know it from the formula for the sum of a geometric progression.
In any way, I assume you know it.
Next step. If w is the root of the equation 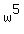 = 1, then the left side in (1) becomes equal to zero,
and you get
= 1, then the left side in (1) becomes equal to zero,
and you get
 = 0. (2)
Since w is different from 1, the factor (w-1) is not zero, and you can cancel it in both sides of (2).
You will get then
= 0. (2)
Since w is different from 1, the factor (w-1) is not zero, and you can cancel it in both sides of (2).
You will get then
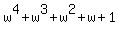 = 0,
exactly what should be proved.
Thus the proof is completed.
= 0,
exactly what should be proved.
Thus the proof is completed.
Proof 2
If w is the root of the equation w^5 = 1, then 1, w, w^2, w^3, w^4 is the set of ALL 5 (five) roots of this equation.
I proved it for you in my PREVIOUS post.
Now apply the Vieta's theorem:
for any polynomial equation of the degree n with the leading coefficient 1,
the sum of its roots is equal to the coefficient at 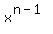 taken with the opposite sign.
Since in the given equation x^5-1 = 0 the coefficient at
taken with the opposite sign.
Since in the given equation x^5-1 = 0 the coefficient at 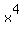 is 0 (zero, ZERO),
the sum of its roots is equal to zero:
1 + w + w^2 + w^3 + w^4 = 0.
It is exactly what has to be proved.
The proof is completed.
is 0 (zero, ZERO),
the sum of its roots is equal to zero:
1 + w + w^2 + w^3 + w^4 = 0.
It is exactly what has to be proved.
The proof is completed.
-------------
Thus you have two (TWO) proofs, to your great satisfaction.