Question 1160269: Marina had an accident with her car and the repair bill came to $900. She didn’t have any emergency fund money and no
extra money in her monthly budget, so she ended up borrowing from a pay-day loan company. As long as she can pay the
loan back at the end of the 30 day period she won’t be charged any interest, technically. However, she did have to pay an
$18 processing fee per $100 that she borrowed.
The end of the month has arrived and Marina was only able to save up $175 to pay off her pay-day loan of $900. This
means she will have to delay payment on the remaining $725 until next month. Besides the delayed payment fee that she
is charged, she will now have to pay interest on the remaining amount. The APR (annual percentage rate) is 47%, but
the interest is compounded daily.
What is the effective interest rate that Marina will actually be paying?
Answer by Theo(13342)   (Show Source): (Show Source):
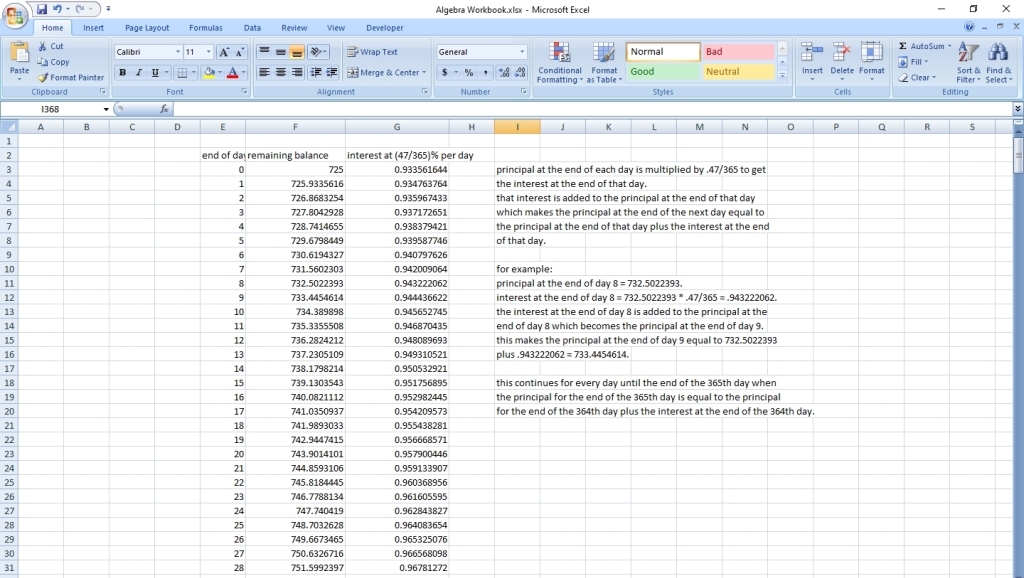
You can put this solution on YOUR website! the repair bill is 900.
there is an 18 dollar processing fee for every 100 dollars that she borrows.
the processing fee on 900 is 9 * 18 = 162 dollars.
at the end of the month, she was able to pay 175 dollars.
that left 725 dollars that she had to borrow at 47% apr compounded daily.
47% apr compounded daily, assuming 365 days in a year, would have an effective interest rate of (1 + .47/365) ^ 365 = 1.599510519 - 1 = .599510519 * 100 = 59.9510519% per year.
the interest rate per day is .47/365 = .0012876712 * 100 = .12876712%.
*****
your solution is an effective interest rate of 59.9510519% per year, based on a nominal rate of 47% per year compounded daily, assuming 365 days in a year.
*****
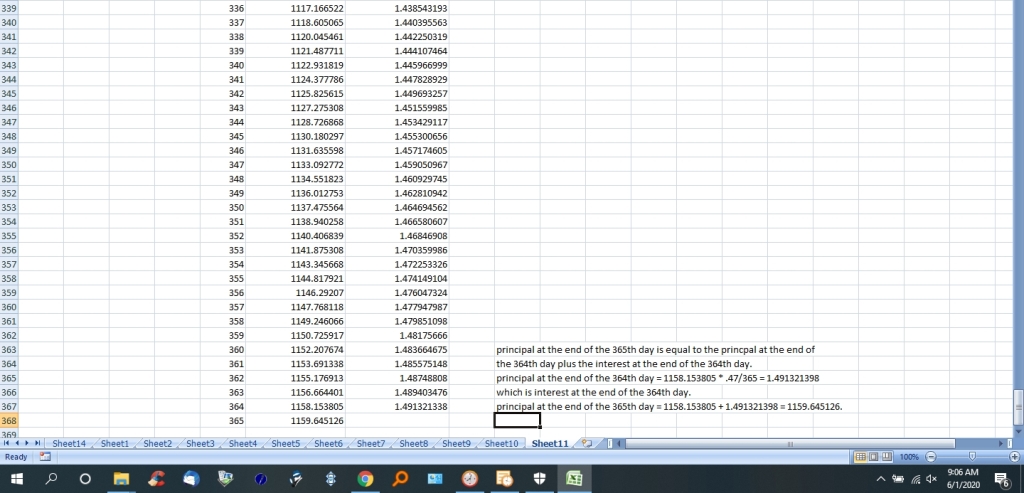
if you assume it took her one whole year before she could pay back the $725 dollars, then she would have to pay a total of 1.599510519 * 725 = 1159.645126 dollars.
750 of that would be the principal and the rest would be interest on the principal.
here's two pictures, the first of the first few day calculations, and the second of the last few day calculations.
|
|
|