Question 1160234: "TJ has 2 types of cereal bar: raisin and nut bars. each raisin bar is 12p more than a nut bar. 9 raisin bar and 12 nut bar cost £5.28.
1) how much more do nine raisin bars cost than nine nut bars?
2) how much does a raisin bar cost?"
I need an answer but for a 9-year-old. Is there a simplified way of answering? The question is from an 11-year-old Exam and I don't think its as complicated as I have explained to my brother or the explanation I have already found online on this website. Help, please?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The answer to (1) is more than easy:
if one raisin bar is 12p more than one nut bar, then 9 raisin bars cost 12p times 9 more than 9 nut bars.
12p 9 times is 108p. ANSWER to part (1)
Isn't it self-evident ? What is the sense to ask about obvious things ?
====================
To answer question (2), put all 12 + 9 = 21 bars in a row.
Close to each nut bar place 12p (mentally).
Then you will have 21 groups: 9 groups contain raising bars only, each group;
12 groups contain nut bar and 12p, each group.
So, you have 21 groups, and each of them "costs" the same amount.
To keep everything in equilibrium, you must add 12*12p = 144p to £5.28, giving you 528 + 144 = 672p.
Last step is to divide 672p by 21 to get the price of one raisin bar 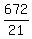 = 32p. = 32p.
It is your ANSWER: one raisin bar costs 32p.
Solved.
Is it clear to you and to your 9-years brother ?
/\/\/\/\/\/\/\/\/
This problem is close to coin problems.
For coin problems and their detailed solutions see the lessons in this site:
- Coin problems
- More Coin problems
- Solving coin problems without using equations (*)
- Kevin and Randy Muise have a jar containing coins
- Typical coin problems from the archive
- Three methods for solving standard (typical) coin word problems
- More complicated coin problems
- Solving coin problems mentally by grouping without using equations (*)
- Non-typical coin problems
- Santa Claus helps solving coin problem
- OVERVIEW of lessons on coin word problems
You will find there the lessons for all levels - from introductory to advanced,
and for all methods used - from one equation to two equations and even without equations.
For methods without using equations, see the lessons marked (*) in the list.
A convenient place to quickly observe these lessons from a "bird flight height" (a top view) is the last lesson in the list.
Read them attentively and become an expert in this field.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Coin problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A "simplified" way of answering the question for a 9-year-old is whatever "works" for the 9-year-old.
We can only guess what might work well. Certainly we don't want to use formal algebra....
Here are my thoughts for explaining this to a 9-year-old.
The problem is well presented for solving by a 9-year-old, in that the first question asked is key to one method for making solving the problem relatively easy.
Each raisin bar costs 12p "extra"; so the "extra" cost for the 9 raisin bars is 9*12p = £1.08.
ANSWER to the first question: 9 raisin bars cost £1.08 more than 9 nut bars.
We're done with the first question. Now we use that result to solve the rest of the problem.
Having accounted for the "extra" cost of the raisin bars, we have left 9+12=21 cereal bars, each costing the same amount; and the amount remaining is £5.28=£1.08 = £4.20. So the cost of each nut bar is £4.20/21 = 20p.
So each nut bar costs 20p, and each raisin bar costs 20p+12p = 32p.
ANSWER to second question: A raisin bar costs 32p.
|
|
|