Question 116017: Can someone help me with this graphing?
Describe the transformations on the following graph of f(x)=log(x). State the replacement of the verticle asymptote and x-intercept after the transformation. For example, "left 1" or stretched vertically by a factor of 2" or descriptions.On my graph i see a line from -2 on the y axis and 10 on the x-axis
a)g(x)=log(x+2)
Description of transformation:
Vertical asymptote:
x-intercept in (x,y) form:
b) g(x)= -log(x)
Description of transformation:
Vertical asymptote:
x-intercept in (x,y)form:
Need help asap
Thankyou
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! a)
From the graph of  , we can see that only positive x values will work. In other words, the domain of f is (0, ). Now let's find the domain of  :
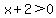 Set the inner expression greater than zero
 Subtract 2 from both sides
 Combine like terms on the right side
So that means x must be greater than -2
So here is the domain in interval notation: (-2,)
Notice how the endpoint of the domain has been shifted to the left two units. So what this did was simply shift every x value 2 units to the left
----------------------------------
Answer:
So the transformation  shifts the entire graph of two units to the left
Notice if we graph  and  , we get
 Graph of (red) and (green)
and we can visually verify the transformation
Vertical Asymptote:
From the graph, we can see that the vertical asymptote is  for . Since we've shifted the graph 2 units to the left, we've also shifted the vertical asymptote 2 units to the left.
----------------------------------
Answer:
So the vertical asymptote for is 
We can visually verify this if we look at the graph above
x-intercept in (x, y) form:
From the graph, we can see that the x-intercept of is (1,0). Since we've shifted everything two units to the left, the x-intercept shifts two units to the left also.
So subtract 2 from 1 to get
(1-2,0)---->(-1,0)
----------------------------------
Answer:
So the x-intercept of is (-1,0)
Once again, we can visually verify this if we look at the graph above
b)
Description of transformation:
Remember, is the same as y. So this means 
Now if we negate both sides to get 
So is simply making each y coordinate becomes it's opposite. So something like (0,2) becomes (0,-2) and (3,-2) becomes (3,2), etc
----------------------------------
Answer:
So what's happening is that the graph is being reflected over the x-axis
Notice if we graph and , we get
 Graph of (red) and  (green)
and we can visually verify the transformation
Vertical Asymptote:
From the graph, we can see that the vertical asymptote is . Since the transformation reflected the graph across the x-axis, the vertical asymptote of is the same as the vertical asymptote of
----------------------------------
Answer:
So the vertical asymptote of is
We can verify this by looking at the graph above
x-intercept in (x, y) form:
From the graph, we can see that the x-intercept of is (1,0). Since we've reflected everything with respect to the x-axis, the point on the x-axis is not affected. In other words the x-intercept of is the same as the x-intercept of
----------------------------------
Answer:
So the x-intercept of is (1,0)
Once again, we can visually verify this if we look at the graph above
|
|
|
