Question 116016: Describe the transformations on the following graph of f(x)=e^x.
State the placement of the horizontal asymptote and y-intercept after the transformation. For example, “left 1” or “rotated about the y-axis” are descriptions.
a) g(x)=e^x+3
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
Description of transformation:
Remember,  is the same as is the same as  . So this means . So this means  . .
So when we say 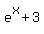 , we're also saying , we're also saying 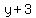 (replace (replace  with y). So this means we're adding 3 to each y value which graphically shows us that we're shifting each y value up 3 units. with y). So this means we're adding 3 to each y value which graphically shows us that we're shifting each y value up 3 units.
----------------------------
Answer:
So the transformation  simply shifts the entire curve up 3 units. simply shifts the entire curve up 3 units.
Notice if we graph  and and  , we get , we get
 Graph of Graph of  (red) and (red) and  (green) (green)
and we can visually verify the transformation
Horizontal Asymptote:
Now if we found the asymptote of  , we would find that the asymptote is , we would find that the asymptote is  . Since we're translating each point on . Since we're translating each point on  up 3 units, we're also translating the horizontal asymptote up 3 units. up 3 units, we're also translating the horizontal asymptote up 3 units.
----------------------------
Answer:
So the new horizontal asymptote is  . .
Also, you can visually verify this answer by looking at the graph above
y-intercept in (x, y) form:
If we let x=0 and plug it into  , we get , we get
 Plug in x=0 Plug in x=0
 Raise e to the zeroth power to get one. Remember any number x to the zeroth power is always one (ie Raise e to the zeroth power to get one. Remember any number x to the zeroth power is always one (ie  ) )
So for  the y-intercept is (0,1) the y-intercept is (0,1)
Now if  translates each y value up 3 units, then simply add 3 to the y-coordinate of the y-intercept to get translates each y value up 3 units, then simply add 3 to the y-coordinate of the y-intercept to get
(0,1+3)---->(0,4)
----------------------------
Answer:
So the new y-intercept is (0,4)
Once again, you can visually verify this answer by looking at the graph above
|
|
|