SOLUTION: At the end of the day, a pharmacist counted and found she has 4/3 as many prescriptions for antibiotics as she did for cough medicines. She had 84 prescriptions for the two types

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: At the end of the day, a pharmacist counted and found she has 4/3 as many prescriptions for antibiotics as she did for cough medicines. She had 84 prescriptions for the two types       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1160146: At the end of the day, a pharmacist counted and found she has 4/3 as many prescriptions for antibiotics as she did for cough medicines. She had 84 prescriptions for the two types of medicine. How many prescriptions did she have for cough medicine?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52855) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let x = # of C-prescriptions.

Then the number of A-prescriptions is  %284%2F3%29x.


From the condition, you have this equation

    x + %284%2F3%29x = 84.


Simplify and solve


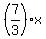    %287%2F3%29x = 84

    x = %283%2F7%29%2A84 = 3*12 = 36.


ANSWER.  36 C-prescriptions and %284%2F3%29%2A36 = 4*12 = 48 A-prescriptions.

Solved.

/\/\/\/\/\/\/\/

Remember !


    If a student dislikes fractions, it is a SERIOUS DEFICIENCY in his (or her) mathematical education !


    If you, unfortunately, belong to this category, MAKE EVERYTHING you can to learn manipulating FREELY with the fractions !


    Remember : fractions are friends of a human !  They want and they can be your personal friends !



Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


Since many students dislike working with fractions, here is another way to set up and solve this problem.

The statement of the problem says there are 4/3 as many prescriptions for antibiotics as there are for cough medicines. A direct translation of that information into algebraic expressions would have x as the number of prescriptions for cough medicines and (4/3)x for the number of prescriptions for antibiotics.

A different approach would be to translate the "....4/3 as many..." into "...a ratio of 4:3...". Then we can use 3x for the number of prescriptions for cough medicines and 4x for the number of prescriptions for antibiotics.

Now the algebra is easier:

3x%2B4x+=+84
7x+=+84
x+=+84%2F7+=+12

The number of prescriptions for cough medicines is 3x = 3(12) = 36.