SOLUTION: Use the given information to determine the values of sine 2 theta​, cosine 2 theta, and tangent 2 theta. cos theta=8/17; The terminal side of theta lies in quadrant IV.

Algebra ->  Conversion and Units of Measurement -> SOLUTION: Use the given information to determine the values of sine 2 theta​, cosine 2 theta, and tangent 2 theta. cos theta=8/17; The terminal side of theta lies in quadrant IV.      Log On


   

Question 1160136: Use the given information to determine the values of sine 2 theta​, cosine 2 theta, and tangent 2 theta.
cos theta=8/17; The terminal side of theta lies in quadrant IV.
Found 3 solutions by MowMow, MathTherapy, ikleyn:
Answer by MowMow(42) About Me  (Show Source):
You can put this solution on YOUR website!
CosΘ = 8/17, Θ = -61.9275 degrees
Sin2Θ = 0.8304
Cos2Θ = -0.5571
Tan2Θ = -1.4907

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

Use the given information to determine the values of sine 2 theta​, cosine 2 theta, and tangent 2 theta.
cos theta=8/17; The terminal side of theta lies in quadrant IV.
I do believe you need the EXACT values.

First, this is an 8-15-17 PYTHAG TRIPLE. Therefore, based on the fact that theta is in Quadrant IV, and that:  we get: 

Now, I can't determine if you want:

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
Use the given information to determine the values of sin(2*theta)​, cos(2*theta), and tan(2*theta).
cos theta=8/17; The terminal side of theta lies in quadrant IV.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


        The solution in the post by @MowMow has two deficiencies.

        First, it is FATALLY incorrect.

        Second, in his post, the educational part of the solution disappeared in full.
        So, I came to provide a correct solution to this problem in the form as it should be
        (as it is expected to be). 


Since  cos%28theta%29 = 8/17  and angle theta is in quadrant IV,

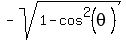    sin%28theta%29 = -sqrt%281-cos%5E2%28theta%29%29 = -sqrt%281-%288%2F17%29%5E2%29 = -sqrt%28%2817%5E2-8%5E2%29%2F17%5E2%29 = 

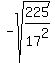                     = -sqrt%28%28289-64%29%2F17%5E2%29 = -sqrt%28225%2F17%5E2%29 = -15%2F17.


Notice that we us sign  '-'  at the square root since angle theta is in quadrant IV, 
where 'sin' is negative.


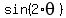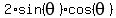Now  sin%282%2Atheta%29 = 2%2Asin%28theta%29%2Acos%28theta%29 = 2%2A%28-%2815%2F17%29%29%2A%288%2F17%29 = -240%2F289 = -0.8304.

     (compare this correct approximate value with incorrect value of 0.8304 in the post by @MowMow).



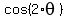For  cos%282%2Atheta%29,  use the formula

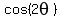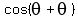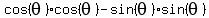     cos%282theta%29 = cos%28theta+%2B+theta%29 = cos%28theta%29%2Acos%28theta%29-sin%28theta%29%2Asin%28theta%29 = 

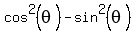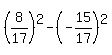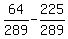                       = cos%5E2%28theta%29-sin%5E2%28theta%29 = %288%2F17%29%5E2+-+%28-15%2F17%29%5E2 = 64%2F289-225%2F289 =  -161%2F289 = -0.5571.



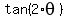For tan%282%2Atheta%29,  use

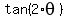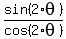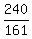     tan%282%2Atheta%29 = sin%282%2Atheta%29%2Fcos%282%2Atheta%29 = %28%28-240%2F289%29%29%2F%28%28-161%2F289%29%29 = 240%2F161 = 1.4907.

     (compare this correct approximate value with incorrect value of -1.4907 in the post by @MowMow).

Solved, and you have clear instructions/guidance on how to do the solution.


/////////////////////////////////////////////////////


@MowMow, it is clear from your post, that you

    - don't know right-angled triangles
    - don't know Pythagorean triangles
    - do not understand the meaning of this assignment
    - and do'n't know (have no idea) on how to solve it correctly.

I observed your contribution to the forum,

and with 179% confidence I can say that you have no necessary knowledge to be a Math tutor.

I ask you STOP posting to this forum.