|
Question 1160127: Write an equation for a rational function with:
Vertical asymptotes at x = -6 and x = -4
x intercepts at x = -1 and x = -3
Horizontal asymptote at y = 7
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
All the parts of this problem are straightforward, and the reasoning makes sense.
Memorize the rules about what makes x-intercepts and vertical asymptotes; but also understand why the rules are what they are.
An x-intercept means the graph crosses (or touches) the x-axis. That means the y value, which is the function value, is 0. In a rational function, the function value is zero whenever the numerator is 0 (unless the denominator is also zero for the same x value).
This function has x-intercepts at x=-1 and x=-3. That means the numerator of the rational function must contain factors of x+1 and x+3. (The factor x+1 means the numerator will be 0 when x = -1; the factor x+3 means the numerator will be 0 when x = -3.)
A vertical asymptote means the function is undefined for that value of x. In a rational function, that means there is a factor in the denominator that is zero for that value of x.
This function has vertical asymptotes at x = -6 and x = -4; that means the denominator has factors of (x+6) and (x+4).
At this point we have satisfied the requirements for the x-intercepts and vertical asymptotes; our function is of the form
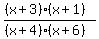
A horizontal asymptote means that for very large positive or very large negative values the function approaches a constant value. In the rational function we have at this point, for very large x values the "x" terms dominate (the constants become insignificant), and the function value approaches  , so the horizontal asymptote is y=1. To get a horizontal asymptote of y=7, we simply add a constant factor of 7 to the numerator.
The function we are looking for is then
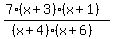
Here is a graph (window -10,2,-5,5) showing the two x-intercepts:
And here is another (window -10,2,-300,300) showing the vertical asymptotes at x=-6 and x=-4:
Answer by MathLover1(20850)  (Show Source):
|
|
|
| |
