.
Let x, y and z be the dimensions of the box.
Then the top and the bottom both (each) have the area xy = 252 in^2;
the front and the back both (each) have the area yz = 105 in^2;
and the two other opposite side faces have the area xz = 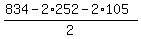 = 60 in^2, each.
NOW
the square of the volume of the box is
V^2 = (xy)*(yz)*(xz) = 252*105*60 = 1587600.
Hence, the volume itself is the square root from this value V =
= 60 in^2, each.
NOW
the square of the volume of the box is
V^2 = (xy)*(yz)*(xz) = 252*105*60 = 1587600.
Hence, the volume itself is the square root from this value V = 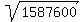 = 1260 cubic inches.
= 1260 cubic inches.
Solved.
-----------------
As you see, the solution is entirely build on using this trick
+--------------------------------------------------------------------------+
| |
| the square of the volume = the product of the areas of the three faces. |
| |
+--------------------------------------------------------------------------+
If you know the trick (as you learned it now, after my explanations),
you will be able to easily solve any similar problem.
Solved, calculated, explained and completed.