Question 1159845: Let L be the linear operator in R^2 defined by
L(x)=(2x1+1x2,0x1+0x2)^T
Find bases of the kernel and image of L.
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
Linear operator L acts on vectors 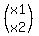 , by mapping each such vector into the vector
L : ---->  .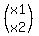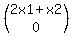
Therefore, the kernel of the operator L are those vectors 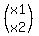, for which 2x1 + x2 = 0.
They are all the vectors of the form  .
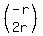They form 1D-space (= actually, a line) spanned on the vector (-1,2) on the standard coordinate plane.
It is the same as to say that the kernel is the line 2y = -x on standard (x,y) coordinate plane, or, equivalently,
the line x + 2y = 0.
The image of this operator L is the 1D-space {(x,0)} - same as the x-axis on the standard coordinate plane (x,y).
--------------
Answered, explained, solved and completed.
/\/\/\/\/\/\/\/\/
Hey, if you really are a student, learning Linear Algebra, can you post me the names of the books/textbooks,
recommended to you by your teacher/professor/lecturer ?
May be, I will be able to add my recommendations to your list.
|
|
|
