Question 1159776: A gift has the dimensions of 𝟓𝟎 𝐜𝐦 × 𝟑𝟓 𝐜𝐦 × 𝟓 𝐜𝐦. You have wrapping paper with dimensions of 𝟕𝟓 𝐜𝐦 ×
𝟔𝟎 𝐜𝐦. Do you have enough wrapping paper to wrap the gift? Why or why not?
Found 4 solutions by josgarithmetic, ikleyn, jim_thompson5910, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Comparing areas, the package is 4350 square cm, and the paper is 4500 square cm. At least enough paper. (Not trying to account for overlap for taping)
Answer by ikleyn(52782)  (Show Source):
You can put this solution on YOUR website! .
Let's assume for a minute that such wrapping is possible.
I will show that it leads to a contradiction, which will prove that wrapping is not possible.
Let's assume that the box is wrapped.
Mark the point at the center of the 50 cm by 35 cm face of the box.
Using pencil, draw the straight segments along the longest path on the box surface until you return to the same point,
moving perpendicularly to 35 cm edges.
The length of this longest path is 25 + 5 + 50 + 5 + 25 = 110 centimetres.
If you then un-wrap the paper, you will get a straight line segment on it, whose total length is 110 centimetres.
But it is NOT POSSIBLE : the longest straight segment on this piece of paper is its diagonal,
whose length is 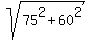 = 90.05 centimetres (rounded).
This contradiction PROVES my statement.
---------------
Here in the forum some tutors assume "it may be this way, or may be that way . . . "
I hope you do understand, that the solution I found for you is a
**************
* BRILLIANT *
**************
and there is NO any other way to discuss . . .
Actually, it is a brilliant problem and a brilliant solution of the Math circle level,
for a special session of the Math circle.
/\/\/\/\/\/\/\/
Let me tell you one story from Physics. // Once upon a time . . .
In one country, let's call it "country N", were there two physicists, X and Y.
The X was a worldwide recognized, very authoritative person (in that sense that he was
very respectful for his knowledge, skills and talents - a kind of moral and scientific authority).
The Y was, how to say it, a row professor, without world wide fame.
And there was the third physicist, Z, in an abroad country.
It happened, that Z made a world-wide scale discovery in Physics, for which he obtained the Nobel prize.
When Y learned about it, he came to X (they were close friends) and said
"my dear X, I am very disappointed by myself. The matter is that I made this discovery two years
before Z did it; but I didn't give importance to it and did not publish it . . . "
For it, master X replied: "Do not tell to ANYBODY about it.
Because it is not a shame do not make this discovery --- thousands of people did not make it.
But it is a real shame TO MAKE this discovery and do not give importance to it."
------------
End of the story.
Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website!
It all depends on if you are allowed to cut the wrapping paper. If you can only tape the wrapping paper, and not cut it or tear it, then it is not possible to fold the paper around the entire surface area of the box you want to wrap. This is due to what the tutor @ikleyn has shown.
If you are able to cut/tear the wrapping paper, then the tutor @josgarithmetic points out that the wrapping paper has area of 75*60 = 4500 square cm while the box has surface area 4350 as shown by the formula below
SA = 2*(L*W+L*H+W*H)
SA = 2*(50*35+50*5+35*5)
SA = 4350
Since the wrapping paper has more area compared to the box's surface area, this means we have enough paper to be able to cover all of the box. You would have to cut the wrapping paper into various smaller pieces, and then rearrange them as you would a puzzle. There will be leftover wrapping paper.
So in summary, it depends on the conditions your teacher has provided. I would ask them to see if cuts/tears are allowed.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! A gift has the dimensions of 𝟓𝟎 𝐜𝐦 × 𝟑𝟓 𝐜𝐦 × 𝟓 𝐜𝐦. You have wrapping paper with dimensions of 𝟕𝟓 𝐜𝐦 ×
𝟔𝟎 𝐜𝐦. Do you have enough wrapping paper to wrap the gift? Why or why not?
Simply, and based on how gift boxes are wrapped, there's NOT enough wrapping paper.
The gift box's top and bottom have the largest surface areas, which means that the top and bottom would have the longest sides being 50 cm each, or a total length of
2(50) or 100 cm. The sides have not even been taken into consideration, just the top and bottom of the gift box.
Now, when the longer side of the wrapping paper is folded over, will it be enough to cover at least 100 cm? No!!
Just have a little imagination and it'll become quite clear to you!
|
|
|
