SOLUTION: Bert traveled 72 miles across the state through rain at a reasonable speed. If it had been sunny, he would have driven an average of 20 miles per hour faster, and would have arriv

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: Bert traveled 72 miles across the state through rain at a reasonable speed. If it had been sunny, he would have driven an average of 20 miles per hour faster, and would have arriv      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1159329: Bert traveled 72 miles across the state through rain at a reasonable speed. If it had been sunny, he would have driven an average of 20 miles per hour faster, and would have arrived at his destination 24 minutes sooner. How long did his trip take him in the rain? How fast was he driving in the rain?
Hint: First solve a quadratic equation. Then write two equations with two unknowns.
Found 3 solutions by josgarithmetic, jim_thompson5910, ankor@dixie-net.com:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
                 SPEED       TIME        DISTANCE

IN RAIN           r          72/r           72

IF SUNNY         r+20        72/(r+20)      72

DIFFERENCE                  2%2F5

72%2Fr-72%2F%28r%2B20%29=2%2F5
.
.
r%5E2%2B20r-3600=0
.
.
highlight%28r=-10%2B10%2Asqrt%2837%29%29 about 50.83.
and you can evaluate the time from this.

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

For anyone curious where @josgarithmetic got the 2/5 from, it's because
24 minutes = (24 min)*(1 hr/60 min)
24 minutes = (24/60) hour
24 minutes = ( (2*12)/(5*12) ) hour
24 minutes = 2/5 of an hour

Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
Bert traveled 72 miles across the state through rain at a reasonable speed.
If it had been sunny, he would have driven an average of 20 miles per hour faster, and would have arrived at his destination 24 minutes sooner.
:
let s = speed in the rain
let t = drive time in the rain
change 24 min 24/60 = .4 hrs, then
(s+20) = sunny speed
(t-.4) = sunny driving time)
Two distance equations
s*t = 72
for substitution
s = 72/t
and
(t-.4)*(s+20) = 72
FOIL
ts + 20t - .4s - 8 = 72
we know ts = 72
72 + 20t - .4s - 8 = 72
-72 from both sided
20t - .4s - 8 = 0
simplify, divide by .4
50t - s - 20
replace s with (72/t)
50t - 72/t - 20 = 0
multiply by t
50t^2 - 72 - 20t = 0
A quadratic equation
50t^2 - 20t - 72 = 0
Using the quadratic formula I got a postive solution of
t = 1.41655 hrs or 1 + .41655*60 = 1 hr 25 min, his time in the rain
:
How fast was he driving in the rain?
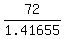72%2F1.41655 = 50.8 mph
:
:
Check this, find his sunny speed. 50.8 + 20 = 70.8 mph
Find his sunny time: 72%2F70.8 = 1.0169 or 1 + .0169*60 = 1 hr 1 min
Which ia 24 min faster than the time in rain


Hint: First solve a quadratic equation. Then write two equations with two unknowns.