Question 1159320: Jotham needs 70 liters of a 50% alcohol solution. He has a 30% solution and an 80% solution available. How many liters of the 30% solution and how many liters of the 80% solution should he mix to make the 50% solution?
Found 3 solutions by ikleyn, Alan3354, MathTherapy:
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jotham needs 70 liters of a 50% alcohol solution. He has a 30% solution and an 80% solution available.
How many liters of the 30% solution and how many liters of the 80% solution should he mix to make the 50% solution?
~~~~~~~~~~~~~~~~
Let x = the volume of the 80% solution needed, in liters.
Then the volume of the 30% solution to mix is (70-x) liters.
The equation to find x is THIS
0.80x + 0.30*(70-x) = 0.50*70,
It says that the volume of the pure alcohol in ingredients is equal to the volume of the pure alcohol in the final mixture.
From this equation, express x and calculate
x = 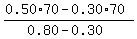 = 28.
ANSWER. 28 liters of the 80% solution and the rest, 70-28 = 42 liters, of the 30% solution. = 28.
ANSWER. 28 liters of the 80% solution and the rest, 70-28 = 42 liters, of the 30% solution.
Solved.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Jotham needs 70 liters of a 50% alcohol solution. He has a 30% solution and an 80% solution available. How many liters of the 30% solution and how many liters of the 80% solution should he mix to make the 50% solution?
------------
t = amount of 30%
e = amount of 80%
--------------
t + e = 70 ----- total solution
0.3t + 0.8e = 0.5*70 ---- total alcohol
---------
3t + 8e = 350
3t + 3e = 210
-------------------- Subtract
5e = 140
e = 28 liters
t = 42 liters
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! Jotham needs 70 liters of a 50% alcohol solution. He has a 30% solution and an 80% solution available. How many liters of the 30% solution and how many liters of the 80% solution should he mix to make the 50% solution?
Tutor @IKLEYN is correct about equal amounts being mixed when % of desired mixture is midway between %s of available solutions.
In her explanation she uses 50% as the desired solution, but mistakenly uses 20% as one of the available solutions, instead of 30%.
With desired solution % being 50, and available solution %s being 30 and 80, correct amount of 80% solution to mix is:  . .
|
|
|