SOLUTION: The doubling period of a bacterial population is 15 minutes. At time t= 120 minutes, the bacterial population was 60000. What was the initial population at time t=0 ?

120 minutes comprise 8 times 15-minute periods.


So, 120 minutes comprise 120/15 = 8 doubling periods.


When we go one doubling period back, from 120 minutes to 105 minutes, we should divide the current population size by the factor of 2.


When we go 8 doubling periods back, from 120 minutes to the very beginning, we should divide the population of 60000 by ,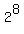 

which gives the initial population  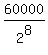=  = 234.375 = 234 (rounded).


From 120 minutes to 5 full hours, we have 3 hours = 3*4 = 12 doubling periods.


Therefore, the size of the bacterial population after 5 hours is 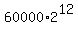  = 245760000.