Question 1158642: Set-Builder Notation and Interval Notation.
Suppose A={x is an element of real number: -2 less than or equal to X < 5 } and B= (-1, 6]
1. Find A U B and give the answer in interval notation. (7marks)
2. Write A n (intersection) B as one set using set builder notation (4marks)
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! Set-Builder Notation and Interval Notation.
Suppose A={  is an element of real number:  } and B= ( ,  ]
=> = ,, , , , ,
=> =,,,,,,, ,
1. Find A U B and give the answer in interval notation.
means: the new set that contains every element from either of and 
in your case contains every element from and some more, so union is actually set
U ==,,,,,,,,
in interval notation: (, ]
2. Write A (intersection) B as one set using set builder notation.
means: the new set that contains every element that is in both of the input sets; only things inside both of the input sets get added to the new set
in your case all elements of are also elements of , so intersection is actually set
 ∩= =,,,,,,
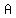{ is an element of real number: }
|
|
|
