SOLUTION: Let X represent the difference between the number of heads and the number of tails when a coin is tossed 33 times. Then P(X=3)=

In this problem, the sum  Heads+Tails  is 33,  while the difference Heads-Tails = 3.


It immediately follows that Heads = 18, Tails = 15.


Therefore, the event X= 3 is EQUIVALENT to event Tails = 15.


Now, P(Tails=15) is (use the formula of probability for the Binomial distribution)


    P(Tails=15) = 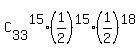 = BINOM.DIST(15, 33, 0.5, FALSE) = 0.120741.    ANSWER


I used the standard EXCEL function to calculate the binomial distribution probability.


        Its second parameter is the "number of trials n"           (n= 33 in this case);  
        the first parameter is the "number of successful trials"   (k= 15 in this case);
        third parameter is "the probability of success in each one single trial"  (p= 0.5 in this case); and 
        the fourth parameter says if you want calculate a single addend or the sum of addends (the single addend in this case).

    Input  "=BINOM.DIST(15, 33, 0.5, FALSE)" into any MS Excel cell in your computer and press enter to get the answer P = 0.120741 immediately.


    On Excel function BINOM.DIST, see its description everywhere, for example

    https://support.office.com/en-us/article/binom-dist-function-c5ae37b6-f39c-4be2-94c2-509a1480770c