Question 1158324: Hi Professor:
I have a question related to the probability, a stock price is currently at $10, what will be the probability the stock price will be above $10 after 5 days? Assume the stock price will be randomly moved according to the following exact percentages: -3%, -2%, -1%, 1%, 2% and 3% (so there are total 6 different possible percentages movement and the movement are purely random among each day).
My approach to this problem is the following: there are total 6 different movement, and the total trials are 5 days, so the total permutations will be 6^5=7776, but I just can't continue the rest due to my limited math knowledge, could you help me out on this?
Thank you for reading my email and I am looking forward to hearing from you soon.
Alex
California
Hi Tutors:
Thank you for answering my questions above (at Answer 781251 ).
I think the answer (781251) just solved one of the permutation, what if the percentage change were repeatable negative percentages, these percentage changes are all independent, so it could have like: -3% every single days, or -3% for 3 days then another 2 days -2%, etc. I wanted to know what are the probability under all the permutations, what are the chances that the stock price at the end of 5th day will be above $10?
again, thanks
Alex
Found 3 solutions by greenestamps, ikleyn, pdream98:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
original response deleted... I'm looking at this further....
----------------------------------------------------------------------
In my earlier attempt at solving this, I tried to simplify the problem by treating all the percent increases and decreases as being relative to the original price. That way, for instance, increases of 3% and 3% would exactly balance decreases of 1%, 2%, and 3%.
However, that is probably not how the problem was intended.
If the percentage increases or decreases are treated as multipliers, there is NO permutation of 5 of the 6 posssible percentage changes that results in an ending price exactly equal to the starting price.
So I looked at the problem again....
Certainly the other tutor missed the point of the problem, finding the percent increase or decrease if each of the changes is applied once.
It appears to me that a purely analytic solution would be extremely tedious, making it necessary to examine each permutation of 5 of the 6 percentage changes.
So I built an excel spreadsheet with all 6^5=7776 permutations of 5 of the 6 and identified the ones that produced a product greater than 1.
ANSWER: 3588 of the 7776 permutations of 5 of the 6 percentage changes produce a product greater than 1. Therefore, the probability that the stock price will be above the original $10 after 5 days is 3588/7776, or about 46.142%.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If  , ,  , ,  , . . . , , . . . , 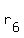 are percentage rates increase/decrease, then the new price after a chain of changes is are percentage rates increase/decrease, then the new price after a chain of changes is
 = = 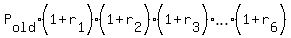 .
What is INTERESTING, after any chain of assigned changes, the value of the product of the growing/decreasing factors
DOES NOT DEPEND of their order in the chain.
It provides the answer in this case: the final growing/decreasing factor is
(1+0.03)*(1+0.02)*(1+0.01)*(1-0.01)*(1-0.02)*(1-0.03) = 0.9986.
Thus, after the chain of changes, you have finally DECREASE of the price by
(1-0.9986)*100 = 0.14%,
I N D E P E N D E N T L Y of the order of changes in the chain.
+----------------------------------------------------------------------------+
| So, after the given chain of changes, the final price of the stock will be |
| |
| 10.00 - 0.0014*10.00 = 9.99 cents (rounded to the closest cent) |
| |
| |
| independently of the order of the pre-assigned changes. ANSWER |
+----------------------------------------------------------------------------+ .
What is INTERESTING, after any chain of assigned changes, the value of the product of the growing/decreasing factors
DOES NOT DEPEND of their order in the chain.
It provides the answer in this case: the final growing/decreasing factor is
(1+0.03)*(1+0.02)*(1+0.01)*(1-0.01)*(1-0.02)*(1-0.03) = 0.9986.
Thus, after the chain of changes, you have finally DECREASE of the price by
(1-0.9986)*100 = 0.14%,
I N D E P E N D E N T L Y of the order of changes in the chain.
+----------------------------------------------------------------------------+
| So, after the given chain of changes, the final price of the stock will be |
| |
| 10.00 - 0.0014*10.00 = 9.99 cents (rounded to the closest cent) |
| |
| |
| independently of the order of the pre-assigned changes. ANSWER |
+----------------------------------------------------------------------------+
Solved.
-------------
Quite unexpected result, isn't it ?
But a correct one (!)
Answer by pdream98(1)   (Show Source): (Show Source):
|
|
|