SOLUTION: Determine {{{(r + s)(s + t)(t + r)}}}, if r, s, and t are the three real roots of the polynomial {{{x^3 + 9x^2 - 9x - 8}}}.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Determine {{{(r + s)(s + t)(t + r)}}}, if r, s, and t are the three real roots of the polynomial {{{x^3 + 9x^2 - 9x - 8}}}.      Log On


   

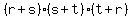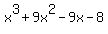Question 1157927: Determine %28r+%2B+s%29%28s+%2B+t%29%28t+%2B+r%29, if r, s, and t are the three real roots of the polynomial x%5E3+%2B+9x%5E2+-+9x+-+8.
Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
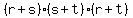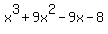Determine %28r%2Bs%29%28s%2Bt%29%28r%2Bt%29, if r, s, and t are the three real roots of the polynomial x%5E3%2B9x%5E2-9x-8.
~~~~~~~~~~~~~~~~~~ 


(r+s)(s+t)(r+t) = ((r + s + t)-t) * ((s + t + r) - r) * ((r + t + s) - s) =


    In the last three factors, replace  r+s+t by -9 (the value opposite to the coefficient at x^2).
    Then continue the equality


= (-9-t)*(-9-r)*(-9-s) = -(9+t)*(9+r)*(9+s) = 

= -(81 + 9t + 9r + tr)*(9+s) = -(729 + 81t + 81r + 9tr + 81s + 9ts + 9rs + trs) = 

= -(729 + 81*(t + r + s) + 9*(tr + ts + rs) + trs) = 


    In the last expression, replace  (t+r+s) by -9 (the value opposite to the coefficient at x^2);
    
    replace  (tr + ts + rs) by -9 (the value of the coefficient at x),

    and replace trs by 8 (the value opposite to the coefficient at the constant term of the polynomial, by Vieta's theorem).  


    You can continue then in this way


= -(729 + 81*(-9) + 9*(-9) + 8) = 73.     ANSWER

Solved.