SOLUTION: log2(3x+4)=5

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: log2(3x+4)=5      Log On


   

Question 1157834: log2(3x+4)=5
Found 4 solutions by MathLover1, MathTherapy, josgarithmetic, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

log%282%2C%283x%2B4%29%29=5.......change to the base 10
log%28%283x%2B4%29%29%2Flog%282%29=5
log%28%283x%2B4%29%29=5log%282%29
log%28%283x%2B4%29%29=log%282%5E5%29...if log same then
3x%2B4=2%5E5
3x%2B4=32
3x=32-4
x=28%2F3-> exact solution
x=9.3333->approximately


Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

log2(3x+4)=5
Because I have ESP, I can tell you that the BASE IS 2.

Is there anything else you need to know?

Answer by josgarithmetic(39625) About Me  (Show Source):
You can put this solution on YOUR website!
--------------------------
log2(3x+4)=5
--------------------------

Maybe log%282%2C%283x%2B4%29%29=5;
2%5E5=3x%2B4
32=3x%2B4
28=3x
x=28%2F3=9%261%2F3

Answer by ikleyn(52855) About Me  (Show Source):
You can put this solution on YOUR website!
.

You start from this equation

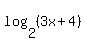    log%282%2C%283x%2B4%29%29 = 5


This equation is equivalent to

    3x + 4 = 2%5E5 = 32.


Therefore,

    3x = 32 - 4

    3x = 28

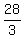     x = 28%2F3 = 91%2F3.    ANSWER

Solved.

Simple enough ?   ---   As simple as it should be.

--------------

Learn this lesson from my post: 

    You do not need to change the base of logarithms from 2 to 10.

    You do not need to change the base of logarithms, at all.


    Do not make excessive operations --- do not make excessive work --- it is only a source for possible errors.

    Do not spend your time for nothing.


    There is an issue of correct STYLE, also.  When you do it, as the other tutor does,
    you only demonstrate that you do not know the subject, the logarithms,

    and do not know how to solve such problems correctly.


    Remember, that a right style is YOUR REPUTATION (!)

-----------------

On logarithms and their properties,  see these introductory lessons
    - WHAT IS the logarithm
    - Properties of the logarithm
    - Change of Base Formula for logarithms
    - Evaluate logarithms without using a calculator
    - Simplifying expressions with logarithms
    - Solving logarithmic equations
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Logarithms".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.