SOLUTION: Two salesmen are visiting houses to sell vacuum cleaners. Together, they can stop at every house in a neighborhood in 2 days, but one salesman covers twice as many houses as the ot

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: Two salesmen are visiting houses to sell vacuum cleaners. Together, they can stop at every house in a neighborhood in 2 days, but one salesman covers twice as many houses as the ot      Log On


   

Question 1157385: Two salesmen are visiting houses to sell vacuum cleaners. Together, they can stop at every house in a neighborhood in 2 days, but one salesman covers twice as many houses as the other. If they work together for one day, how long will the slower salesman take to finish the neighborhood?
Found 4 solutions by greenestamps, josgarithmetic, MathTherapy, ikleyn:
Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


The faster salesman works twice as fast as the slower, so when they work together the faster salesman does 2/3 of the work and the slower salesman does 1/3.

Together they can finish the job in 2 days; so in the 1 day they work together they do half of the job. Of the work done that day, the slower salesman does 1/3 of it.

An equal amount of work remains to be done by the slower salesman alone; and we know he can do 1/3 of that amount of work in 1 day. So it will take him 3 days to finish the job.

Answer by josgarithmetic(39621) About Me  (Show Source):
You can put this solution on YOUR website!
slow man 1/(2x)
fast man 1/x
together 1%2F%282x%29%2B1%2Fx=1%2F2

1%2F%282x%29%2B2%2F%282x%29=1%2F2
3%2F%282x%29=1%2F2
3%2Fx=1%2F1
highlight%28x=3%29----------the slow salesman needs 3 days if alone.






--
--

rechecked
redone & adjusted

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
Two salesmen are visiting houses to sell vacuum cleaners. Together, they can stop at every house in a neighborhood in 2 days, but one salesman covers twice as many houses as the other. If they work together for one day, how long will the slower salesman take to finish the neighborhood?
Is that other person who responded, SERIOUS?

How can both salesmen cover all houses in 2 days, but then the slower salesman can cover the remaining houses in 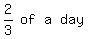matrix%281%2C4%2C+2%2F3%2C+of%2C+a%2C+day%29.

Does he even look over what he posts? I'm sure he doesn't, or if he does, something is SERIOUSLY wrong with him!

Answer by ikleyn(52818) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let x be the rate of work of the slower salesmen in terms of job per day;  

then the rate of work of the faster salesmen is 2x of job per day.


From the condition, we have

    2x + 2(2x) = 1 job,

hence 

    2x + 4x = 1,   or  6x = 1, or  x = 1%2F6  of the job per day   (rate of work of the slower salesmen).


From the other side, working together for 1 day, the two salesmen completed half of the job;
another half remained uncompleted.


So, the time for the slower salesmen to complete this remained half of the job is

    %28%281%2F2%29%29%2F%28%281%2F6%29%29 = 6%2F2 = 3 days.    ANSWER

Solved.