.
In the denominator, you see  .
In order for you will be able to take the square of a number, this number MUST be non-negative.
So, you first need to solve this inequality
.
In order for you will be able to take the square of a number, this number MUST be non-negative.
So, you first need to solve this inequality
 >= 0.
Factor left side
>= 0.
Factor left side
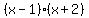 >=0.
Either both factor should be negative, or both factors should be positive.
It gives you the solution set x <= -2 or x >= 1.
Also, x = -2 makes the denominator equal to zero, as well as the value x = 1.
Therefore, you must exclude them from the domain.
Finally, the domain is the union of two open intervals (-oo,-2) U (1,oo). ANSWER
>=0.
Either both factor should be negative, or both factors should be positive.
It gives you the solution set x <= -2 or x >= 1.
Also, x = -2 makes the denominator equal to zero, as well as the value x = 1.
Therefore, you must exclude them from the domain.
Finally, the domain is the union of two open intervals (-oo,-2) U (1,oo). ANSWER
Solved.
---------------
The "solution" by @josgarithmetic is WRONG.
Simply ignore it for your safety.