Question 1157242: If 8 persons are seated at a random in a row. What is the probability that a certain couple
(a) will be together
(b) will not be together
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In all, there are 8! = 8*7*6*5*4*3*2 = 40320 permutations of 8 objects.
If two of them are together, we consider them as one item, and then we have, actually, 7! = 7*6*5*4*3*2 = 5040 different
permutations for seven items, and two permutations inside this par;
so, in all, there are 2*7! permutations for these 8 persons, where these two are together.
Therefore, the answers are
(a) P =  = = 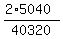 = =  = =  = 0.25;
(b) P = 1 - = 0.25;
(b) P = 1 -  = =  = 0.75. = 0.75.
Solved.
------------------
On Permutations, see introductory lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Problems on Permutations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|