SOLUTION: A rectangular piece of​ cardboard, whose area is 143 square​ centimeters, is made into an open box by cutting a 2​-centimeter square from each corner and turning up the sides

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: A rectangular piece of​ cardboard, whose area is 143 square​ centimeters, is made into an open box by cutting a 2​-centimeter square from each corner and turning up the sides      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1157163: A rectangular piece of​ cardboard, whose area is 143 square​ centimeters, is made into an open box by cutting a 2​-centimeter square from each corner and turning up the sides. If the box is to have a volume of 126 cubic​ centimeters, what size cardboard should you start​ with?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
You can try to draw the figure and label the parts.
If x is one dimension and y the other dimension of the cardboard, then

system%282%28x-4%29%28y-4%29=126%2Cand%2Cxy=143%29

Substituting for y and doing the algebra steps:
24-143%2Fx-x=0
.
.
x%5E2-24x%2B143=0

highlight_green%28%28x-11%29%28x-13%29=0%29
Dimensions of the piece of cardboard, 13 and 11

Answer by ikleyn(52903) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let x an y be the dimensions of the base of the box.


Then the volume is  126 = 2*x*y, which implies

   xy = 126/2 = 63.    (1)


The dimensions of the original cardboard are (x+2*2) = x+4  and  (y+2*2) = y+4, and its area is, therefore

    (x+4)*(y+4) = 143.


Make FOIL

    xy + 4x + 4y + 16 = 143.


Substitute here  xy = 63  from (1), and you will get

    63 + 4x + 4y + 16 = 143,   

or

    x + y = 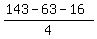%28143+-+63+-+16%29%2F4 = 16.    (2)


So, you need to find two positive numbers, x and y, whose sum is 16  and whose product is 63.


4 seconds, and the solution just came into your mind:  x= 9  and  y= 7.


Then the original dimensions of the cardboard are  9+4 = 13 and  7+4 = 11 centimetres.    ANSWER

Solved // (practically, MENTALLY).