Question 1157104: In Faroe island, a sports training camp provides 3 different sections: one in Squash, one in Football, and one in Basketball. These sections are open to any of the 100 people in the camp. There are 28 students in the Squash section, 26 in the Football section, and 16 in the Basketball section. There are 12 students that are in both Squash and Football, 4 that are in both Squash and Basketball, and 6 are in both Football and Basketball. In addition, there are 2 people taking all 3 sections. If a person chosen at random;
a) If a person chosen at random, the probability that he is not playing in any of these sports sections is
b) If a person chosen at random, the probability that he is playing exactly one sports section is
c) When two people are chosen randomly, the probability that at least 1 is playing in a sports section is
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In Faroe island, a sports training camp provides 3 different sections: one in Squash, one in Football, and one in Basketball.
These sections are open to any of the 100 people in the camp.
There are 28 students in the Squash section, 26 in the Football section, and 16 in the Basketball section.
There are 12 students that are in both Squash and Football, 4 that are in both Squash and Basketball, and 6 are in both Football and Basketball.
In addition, there are 2 people taking all 3 sections. If a person chosen at random;
a) If a person chosen at random, the probability that he is not playing in any of these sports sections is
b) If a person chosen at random, the probability that he is playing exactly one sports section is
c) When two people are chosen randomly, the probability that at least 1 is playing in a sports section is
~~~~~~~~~~~~~~~~
(a) Before answer (a), let me start calculating the probability that a person chosen randomly is playing in some sport section. It is
P(S U F U B) = P(S) + P(F) + P(B) - P(S ∩ F) - P(S ∩ B) - P(F ∩ B) + P(S ∩ F ∩ B) =
= 0.28 + 0.26 + 0.16 - 0.12 - 0.04 - 0.06 + 0.02 = 0.5.
Therefore, the answer to question (a) is the COMPLEMENT probability P(not S U F U B) = 1 - 0.5 = 0.5. ANSWER
(b) P(S only) = P(S) - P(S ∩ F) - P(S ∩ B) + P(S ∩ F ∩ B) = 0.28 - 0.12 - 0.04 + 0.02 = 0.14;
P(F only) = P(F) - P(S ∩ F) - P(F ∩ B) + P(S ∩ F ∩ B) = 0.26 - 0.12 - 0.06 + 0.02 = 0.1;
P(B only) = P(B) - P(S ∩ B) - P(F ∩ B) + P(S ∩ F ∩ B) = 0.16 - 0.04 - 0.06 + 0.02 = 0.08.
Since the three subsets (S only), (F only) and (B only) are disjoint, the answer to question (b) is
P(playing exactly one sport section) = P(S only) + P(F only) + P(B only) = 0.14 + 0.1 + 0.08 = 0.32. ANSWER
(c) P(at least 1 of 2 is playing in a sport section) = 1 - P(1st does not play)*P(2nd does not play) = 1 - 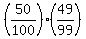 = 0.752525... ANSWER = 0.752525... ANSWER
Solved.
|
|
|