Question 1157079: Find the ordered pair (m,n), where m,n are positive integers satisfying the following equation:

Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
14mn = 55 - 7m - 2n.
Rewrite it in the form
14mn +7m + 2n = 55
Rewrite it one more time in this for
14mn + 7m + 2n + 1 = 56
Rewrite it again in THIS form
(7m + 1)*(2n + 1) = 56.
56 has the following pairs of divisors
(1,56) (2,28), (4,14), (7,8), (8,7), (14,4), (28,2), (56,1).
For each of these pair, write the system of equations (for example, for the pair (4,14)
7m + 1 = 4
2n + 1 = 14
and solve it.
Leave only that pairs that have INTEGER solutions.
Doing exactly with these instructions, you will get the answer.
Actually, the rest part is pure mechanical, therefore, at this point I leave you hoping that your curiosity
is strong enough to complete the job on your own.
You may report me about your progress.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a solution using the method of Diophantine equations.
A basic Diophantine equation is a single equation with two unknowns, in which the solutions are restricted to integers. The requirement that the solutions be integers limits the solutions to only a few, or, as in this case, to a single solution.
This example is a very common type, containing terms in m, n, and mn. The basic techniques for solving that kind of equation are standard.
(1) Solve the equation for one of the variables in terms of the other.




(2) Find the value(s) of n that make the fraction an integer.
m has to be a positive integer, so 7m is an integer. That means 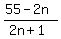 is an integer. is an integer.
It is generally, as in this case, difficult to find values of n that make that expression an integer. So this is what we usually do at this point: write the numerator of the fraction as a multiple of the denominator plus a constant. It's as if we are doing the division and expressing the fraction as an integer plus a remainder.



Now 7m and 1 are integers, so 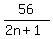 must be an integer; and that means 2n+1 must be a divisor of 56. must be an integer; and that means 2n+1 must be a divisor of 56.
In general, we would look at all the factors of 56 and see what values of n would make 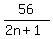 an integer. an integer.
But in this example we can go directly to the solution with a bit of logical reasoning.
For all n, 2n+1 is odd; so 2n+1 must be an odd divisor of 56.
But there is only one odd divisor of 56: 7. (Okay, 1 is an odd divisor of 56; but that would make n=0, and the problem requires m and n to be positive integers.)
So 2n+1 = 7, which makes n=3.
Then  --> m = 1. --> m = 1.
ANSWER: (m,n) = (1,3)
CHECK:
14mn = 14*1*3 = 42
55-7m-2n = 55-7-6 = 42
|
|
|