|
Question 1156837: Hello my name is Karla I am from the 9th grade I am really stuck on this problem.
What is the next smallest integer that is a perfect cube less than -1?
I have tried looking up the answer but I have yet to find what I am looking for. If you can please help me find out the answer. And if you do would you please explain it to me because I am quite confused on it. Thank you to whomever helps me on this math work
-Karla
Found 3 solutions by Theo, ikleyn, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hello Karla.
There is NO "next smallest integer that is a perfect cube less than -1".
It sounds strange, but let's look together.
There is -8 =  . It is an integer, a perfect cube and less than -1.
There is -27 = . It is an integer, a perfect cube and less than -1.
There is -27 = 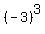 . It is an integer, a perfect cube and less than -1 and less than -8.
There is -64 = . It is an integer, a perfect cube and less than -1 and less than -8.
There is -64 = 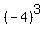 . It is an integer, a perfect cube and less than -1 and less than -27.
There is -125 = . It is an integer, a perfect cube and less than -1 and less than -27.
There is -125 = 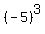 . It is an integer, a perfect cube and less than -1 and less than -64.
And so on . . . . . . . .
For any such example and for any such given integer, there is another integer, which is a perfect cube
and less than -1 and less than the given integer.
It exactly means that THERE IS NO the smallest such an integer. . It is an integer, a perfect cube and less than -1 and less than -64.
And so on . . . . . . . .
For any such example and for any such given integer, there is another integer, which is a perfect cube
and less than -1 and less than the given integer.
It exactly means that THERE IS NO the smallest such an integer.
=================
Hi, Karla, hello again.
I reconsidered my previous answer, which is above.
I looked in GOOGLE, and Google explained me that
- the term "next largest" means "the second after the largest", i.e., in an ordered list in the descending order, "the second from the top".
- "next smallest" means "the next greater than the smallest", i.e., in an ordered list in the descending order, "the second from the bottom".
Now, if you apply this knowledge to your problem, you will see that in this problem, there is NO such a number,
which is "next smallest integer that is a perfect cube less than -1".
There is no such a number, simply because there is no "bottom" in this (ordered) list.
There is "next largest" in this problem, and it is -8 = (-2)^3,
but there is no "next smallest" in this case.
This prose was in use, probably, at the Shakespearean time and at the era of steam and iron.
In modern life, nobody uses this language.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn, while she write many excellent responses to readers' questions, is not expert in the English language. Her contention that there is no answer to the question is not correct. The phrase "next smallest" is different from "smallest".
The other tutor shows what is almost certainly the EXPECTED answer: -8 is the next integer smaller than -1 that is a perfect cube.
However, grammatically the phrasing of the problem is at best confusing, and possibly completely incorrect.
Think about what the phrase "next smallest" means. You have, say, a bunch of spheres of different sizes. There is a smallest sphere; and then the "next smallest" is one that is slightly LARGER than the smallest.
So then the question seems to be self-contradictory in saying that we are looking for THE NEXT SMALLEST integer that is LESS THAN -1.
It is not surprising that you were stuck on this problem, given that it is poorly worded....
|
|
|
| |