.
Find all complex numbers z such that z^2=z with line on top or complex conjugate
~~~~~~~~~~~~~~~~~
It is better and much easier to analyse and to solve this problem in polar trigonometric form.
If z^2 = z complex cojugate, then, firstly, the modulus of z is equal to 1.
In other words, z lies on the unit circle in a coordinate plane.
Next, if the argument of z is polar angle  , then the polar angle of z^2 is
, then the polar angle of z^2 is  ,
while the polar angle of (z conjugate) is
,
while the polar angle of (z conjugate) is  or
or  .
So, we get the equation for the polar angle
Case 1.
.
So, we get the equation for the polar angle
Case 1.  = -
= - , which implies
, which implies  = 0, or
= 0, or  = 0. Then the solution is z = 1.
OR
Case 2.
= 0. Then the solution is z = 1.
OR
Case 2.  =
=  , which implies
, which implies  =
=  . Hence,
. Hence,  =
=  .
ANSWER. There are TWO solutions. One solution is z = 1.
The other solution is z =
.
ANSWER. There are TWO solutions. One solution is z = 1.
The other solution is z = 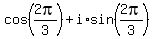 =
= 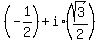 .
.
Solved.