.
The original formulation in the post is FAR from to be PERFECT.
The PERFECT and PRECISELY CORRECT formulation is THIS:
A man walks at 4/5 of his  speed to his office and is late by 5 min.
What is the time it takes to reach his office if he walks at 3/4 of his
speed to his office and is late by 5 min.
What is the time it takes to reach his office if he walks at 3/4 of his  speed.
speed.
I will solve the problem with this formulation.
Let "d" be the distance to the office, and let "u" be the regular speed.
Then the condition produces this time equation
 -
- 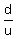 = 5 minutes.
Simplify
= 5 minutes.
Simplify
 -
- 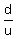 = 5 minutes, or
= 5 minutes, or
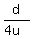 = 5 minutes, or
= 5 minutes, or
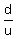 = 4*5 = 20 minutes.
So, his REGULAR time to get the office is 20 minutes.
Now, if he moves at
= 4*5 = 20 minutes.
So, his REGULAR time to get the office is 20 minutes.
Now, if he moves at  of his refular speed, it will take
of his refular speed, it will take 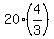 =
=  =
= 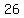
 minutes = 26 minutes and 40 seconds
to get the office. ANSWER
minutes = 26 minutes and 40 seconds
to get the office. ANSWER
Solved.
Same idea can be presented in other form.
Let T be the regular time to get the office (moving at regular speed).
Then with the speed of  of the regular, the time will be
of the regular, the time will be 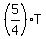 .
Then the condition says us that
.
Then the condition says us that
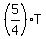 - T = 5 minutes, or
- T = 5 minutes, or
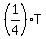 = 5 minutes,
which means T = 4*5 = 20 minutes (regular time).
Then with the speed of
= 5 minutes,
which means T = 4*5 = 20 minutes (regular time).
Then with the speed of  of the regular, the time will be
of the regular, the time will be 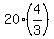 =
=  = 26 minutes and 40 seconds (the same answer).
= 26 minutes and 40 seconds (the same answer).