SOLUTION: A tumor is injected with 0.6 grams of Iodine-125, which has a decay rate of 1.15% per day. To the nearest day, how long will it take for half of the Iodine-125 to decay?

The decay equation in this case is


    M =  = ,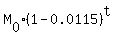


where 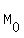 is the original mass, M is the current mass, t is the time in days.


They want you find "t"  from the condition  M = .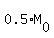


It gives


    0.5 = .


Take the logarithm base 10 from both sides


    log(0.5) = t*log(0.9885).


Hence,  t = 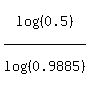 = 59.93 = 60 days  (rounded as required).    ANSWER