Question 1156500: A tour bus normally leaves for its destination at 5:00 p.m. for a 378 mile trip. This week however, the bus leaves at 6:00 p.m. To arrive on time, the driver drives 9 miles per hour faster than usual. What is the bus` usual speed?
Found 4 solutions by ikleyn, josgarithmetic, mananth, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Let x be the regular speed.
Then the time equation is
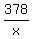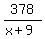 -  = 1.
Multiply both sides by x*(x+9); then reduce to the standard quadratic equation.
Then solve it by any way you want/(you can).
Answer by josgarithmetic(39617)  (Show Source):
Answer by mananth(16946)  (Show Source):
You can put this solution on YOUR website!
A tour bus normally leaves for its destination at 5:00 p.m. for a 378 mile trip. This week however, the bus leaves at 6:00 p.m. To arrive on time, the driver drives 9 miles per hour faster than usual. What is the bus` usual speed?
Let bus` usual be x mph
Distance of the trip = 378 miles
Normal time taken
Time taken = 378/x
Speed increased by 9 mph
speed = (x+9) mph
Time taken = 378/(x+9)
Difference in time = 1 hour ( started one hour late
(378(x+9)-378x)/(x(x+9)) = 1}}}
378x + 3402 -378x = x^2+9x
x^2+9x -3402=0
(x+63)(x-54)=0
x=-63 or 54 . Ignore negative value
normal speed = 54 mph
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You should know how to set up and solve the problem using formal algebra, as shown by the other tutors. Note, however, that with that path you end up having to solve a quadratic equation by factoring by finding two numbers whose difference is 9 and whose product is 3402.
So if a formal algebraic solution is not required, you can find the answer faster by finding two integer factorizations of 378 that satisfy the conditions of the problem.
378 = 2*3*3*3*7
Playing with that prime factorization to find ways to get 378 as a product of two integers finds what we need: 54 times 7 and 63 times 6.
That gives us 378 miles = 7 hours at 54mph or 6 hours at 63mph.
So the regular speed of the bus is 54mph.
|
|
|
