SOLUTION: A Ferris wheel is 20 meters in diameter and boarded from a platform that is 1 meters above the ground. The six o'clock position on the Ferris wheel is level with the loading platfo

This Ferris wheel is a circle of the radius of 10 meters, and its center O is at the height of 11 meters above the ground.


Imagine horizontal line at the level of 19 meters over the ground.

It is 8 meters above the center.


This horizontal line intersect the circle at two points, A and B.

Consider the triangle with the vertices O, A and the point C, which is the middle of the segment AB.


This triangle is a right angled triangle.  Its hypotenuse is the radius OA of 10 meters long.

Its leg OC is of 19-11 = 8 meters long.


Hence,  cos(x) = 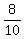 = 0.8,  where x is the angle AOC.


It gives  x = arccos(0.8) = 0.64 radians.


Thus the central angle AOB  is 2x = 2*0.64 = 1.28 radians.


So, the time the person will be higher than 19 meters, can be found from the proportion


     = 


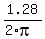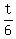    t =  =  = 1.23 minute,  or about 1 minute and 14 seconds.    ANSWER