There is no need to multiply that out, collect terms and write in descending
order. But I went ahead and did it anyway, and got:
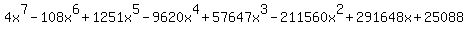 So we see that the degree is 7, the largest exponent of x.
However, we could have told that by observing that the factor (x-8)³ would
contribute a term in x³, the factor (x²+49) would contribute a term in x²
and the factor (4x²-12x-1) would contribute a term in x², so we add the
powers 3+2+2=7 and know that the degree is 7 without multiplying it out.
To find all the zeros, we set the right side of P(x) equal to zero and use the
zero-factor property:
So we see that the degree is 7, the largest exponent of x.
However, we could have told that by observing that the factor (x-8)³ would
contribute a term in x³, the factor (x²+49) would contribute a term in x²
and the factor (4x²-12x-1) would contribute a term in x², so we add the
powers 3+2+2=7 and know that the degree is 7 without multiplying it out.
To find all the zeros, we set the right side of P(x) equal to zero and use the
zero-factor property:

 (x-8)³ = 0; x²+49 = 0; 4x²-12x-1 = 0
x-8 = 0; x² = 49;
x = 8; x = ±7i;
The 8 has multiplicity 3.
That's because if we wrote
(x-8)³
as
(x-8)(x-8)(x-8) = 0
we would have
x-8=0; x-8=0; x-8=0
x=8; x=8; x=8
and 8 would be a zero three times.
The last one won't factor, so we use the quadratic formula
(x-8)³ = 0; x²+49 = 0; 4x²-12x-1 = 0
x-8 = 0; x² = 49;
x = 8; x = ±7i;
The 8 has multiplicity 3.
That's because if we wrote
(x-8)³
as
(x-8)(x-8)(x-8) = 0
we would have
x-8=0; x-8=0; x-8=0
x=8; x=8; x=8
and 8 would be a zero three times.
The last one won't factor, so we use the quadratic formula







 So the zeros are
8 with multiplicity 3
7i with multiplicity 1
-7i with multiplicity 1
So the zeros are
8 with multiplicity 3
7i with multiplicity 1
-7i with multiplicity 1
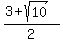 with multiplicity 1
and
with multiplicity 1
and
 with multiplicity 1
Edwin
with multiplicity 1
Edwin