Question 1155916: Every 15 minutes, buses leave from a certain point in both directions.
A traveler who is on foot and leaves at the same time as one of the buses will meet a bus driving towards him after 12 1/2 minutes.
When will another bus overtake him?
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Every 15 minutes, buses leave from a certain point in both directions.
A traveler who is on foot and leaves at the same time as one of the buses will meet a bus driving towards him after 12 1/2 minutes.
When will another bus overtake him?
~~~~~~~~~~~~~~~~~
In this problem, it is assumed that all buses move with the same rate in each direction.
Let "d" be the distance the bus covers in 15 minutes.
I use the term "the bus", meaning any (or every) of the buses.
Let's consider everything on the coordinate line, and let the bus station is located at x= 0 (point O),
at the origin of this coordinate line. Let A be the point at positive distance "d" from the point O.
At the time moment t= 0, the traveler started from O to A; at the same time moment the bus X,
which moves from A towards O, started from A to O.
The bus spends 15 minutes to get from A to O; and the bus meets the traveler at t = 12.5 minutes.
So, the bus covered  = =  of the distance d, while the traveler covered only of the distance d, while the traveler covered only  of the distance d.
Hence, a) the speed of the bus is 5 times the speed of the traveler, and
b) at the moment they meet each other (t= 12.5 minutes), the traveler is at the distance of the distance d.
Hence, a) the speed of the bus is 5 times the speed of the traveler, and
b) at the moment they meet each other (t= 12.5 minutes), the traveler is at the distance 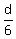 from O.
Now, consider the traveler who continues moving from O to A (and, possible, farther), and the bus Y, which started from O at the time t= 15 minutes.
When the bus Y started from O at t= 15 minutes, the traveler position is from O.
Now, consider the traveler who continues moving from O to A (and, possible, farther), and the bus Y, which started from O at the time t= 15 minutes.
When the bus Y started from O at t= 15 minutes, the traveler position is 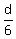 multiplied by the time ratio multiplied by the time ratio  ,
i.e. ,
i.e.  = =  from A.
+-----------------------------------------------------------------------+
| Let u be the speed of the traveler; then 5u is the speed of any bus. |
+-----------------------------------------------------------------------+
For these two objects, we have standard catching up problem.
So, we write equation typical for catching up problem (here "t" is the time moment of catching up,
counted from t= 15 minutes).
5u*t = u*t + from A.
+-----------------------------------------------------------------------+
| Let u be the speed of the traveler; then 5u is the speed of any bus. |
+-----------------------------------------------------------------------+
For these two objects, we have standard catching up problem.
So, we write equation typical for catching up problem (here "t" is the time moment of catching up,
counted from t= 15 minutes).
5u*t = u*t +  .
In this consideration, .
In this consideration,  is the head start for the traveler.
Left side is the distance, covered by bus Y; right side is the distance, covered by the traveler to the catching up moment.
Simplify the equation
5ut - ut = is the head start for the traveler.
Left side is the distance, covered by bus Y; right side is the distance, covered by the traveler to the catching up moment.
Simplify the equation
5ut - ut =  4ut =
4ut =  t =
t =  Transform the right side this way
Transform the right side this way  = = 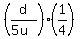 .
Now notice that 5u is the bus speed; therefore the ratio .
Now notice that 5u is the bus speed; therefore the ratio  is 15 minutes (!).
Therefore, t = is 15 minutes (!).
Therefore, t =  = =  minutes = 3.75 minutes.
Resume: The traveler starts from O at t= 0; he meets the opposite bus X at t= 12.5 minutes;
then the bus Y starts from O at t= 15 minutes, and 3.75 minutes later the bus Y catches up the traveler.
ANSWER. The next bus from the bus station will catch up the traveler at t = 15 + 3.75 = 18.75 minutes.
counting the time from the moment the traveler left the bus station. minutes = 3.75 minutes.
Resume: The traveler starts from O at t= 0; he meets the opposite bus X at t= 12.5 minutes;
then the bus Y starts from O at t= 15 minutes, and 3.75 minutes later the bus Y catches up the traveler.
ANSWER. The next bus from the bus station will catch up the traveler at t = 15 + 3.75 = 18.75 minutes.
counting the time from the moment the traveler left the bus station.
Solved.
|
|
|