Question 1155851: Suppose a cylindrical storage tank is to contain V=16,000π cubic feet (about 400,000 gallons) is to be built into the ground to catch runoff water so it needs no top. Suppose, further, that the cost of the base of the tank is $10 per square foot and sides $8.64 per square foot. What dimensions will lead to minimal - cost tank?
Found 2 solutions by josgarithmetic, josmiceli:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  = the diameter of the base = the diameter of the base
Let 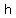 = the height of the tank = the height of the tank
-----------------------------------------
The circumference, 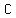 , of the base is: , of the base is:

The area, 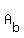 , of the base is: , of the base is:

----------------------------------------
The volume, 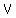 is: is:

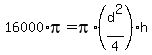


--------------------------------------
The area of the sides, 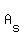 , is: , is:

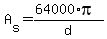
--------------------------------------
The cost, 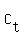 , of the tank is: , of the tank is:


The slope of this curve is:

Set slope = 





 ft ft
and

 ft ft
------------------------------------
The diameter for min cost is 48 ft
The height for min cost is 27.778 ft
-----------------------------------------------
Here's the plot:
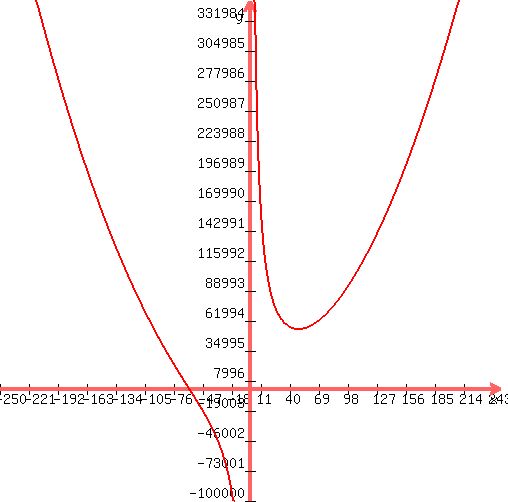
-----------------------------
The min cost is:

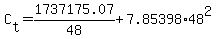


$54,286.72 looks close to min in the plot
Get a 2nd opinion if needed
and check my math
|
|
|